


Next: The method of undetermined
Up: Linear First Order Differential
Previous: Linear First Order Differential
We start with the homogeneous equation
y'+p(t)y=0.
To solve this, we simply divide by y,
y'/y+p(t)=0,
and then integrate
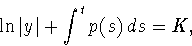
where K is an integration constant.
We take the exponential on both sides:
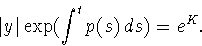
This yields
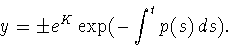
We define a new constant 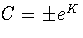 , so we can put the solution in the
form
, so we can put the solution in the
form
| 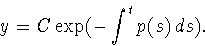 |
(1) |
Now we look at an inhomogeneous equation
The idea of the variation of constants method is to look for a solution in
a form similar to (1). Obviously, something has to change since the
equation has changed. The change is that the constant C is replaced by
a function C(t). So we set
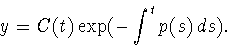
We differentiate using the product and chain rules to find
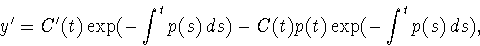
and
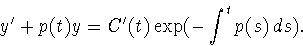
Thus our differential equation becomes
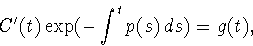
so that
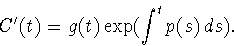
We can then find C(t) by integrating this equation.
The result is evidently the same as what we found using the integrating factor
method, but the ideas leading to the result were different. While for first
order linear equations the integrating factor method and the variation
of constants method are the same, the difference is in how they can be
generalized. The integrating factor method can be generalized to some nonlinear
equations of first order. The variation of constants method, on the other
hand, can be generalized to linear equations of higher order and to linear
systems.



Next: The method of undetermined
Up: Linear First Order Differential
Previous: Linear First Order Differential
Michael Renardy
1998-08-27
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()