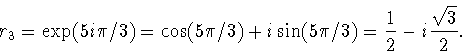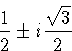Next: About this document ...
Up: No Title
Previous: No Title
Integer roots
If the coefficients of a polynomial are integers, it is natural to look for
roots which are also integers. Any such root must divide the constant term.
We can often ``guess" one or more roots by trying all possibilities.
Example:
r4-2r2-3r-2=0.
If there is an integer root, it must divide -2. This leaves only four
possibilities: 1, -1, 2, and -2. By plugging in, we find that
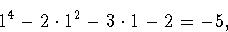
(-1)4-2(-1)2-3(-1)-2=0,
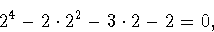
(-2)4-2(-2)2-3(-2)-2=12.
Therefore -1 and 2 are roots, but 1 and -2 are not.
Reducing the degree
If a root has been found, you can reduce the degree of the polynomial to get a
simpler problem for the remaining roots. For example, you know from above
that
r4-2r2-3r-2=0
has the roots -1 and 2. This tells you that the polynomial must contain
the factors r+1 and r-2. You can use the long division algorithm to find
(r4-2r2-3r-2)/(r+1)=r3-r2-r-2,
and
(r3-r2-r-2)/(r-2)=r2+r+1.
Therefore, the remaining roots must solve
r2+r+1=0.
The quadratic formula gives
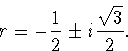
In summary, we have found that the roots of
r4-2r2-3r-2=0
are -1, 2, 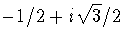 and
and 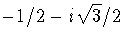 .
.
Multiple roots
It can happen that a polynomial contains the same linear factor more than once.
For instance,
r3-r2-r+1=(r-1)2(r+1).
Since the factor r-1 appears twice, we call 1 a double root of the polynomial,
while -1 is a simple root. Note that
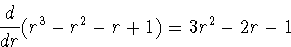
also has a root at r=1. This happens in general: If a polynomial P(r)
as a k-fold root at r=c, then
P(c)=P'(c)=...=P(k-1)(c)=0,
but
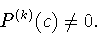
If roots are counted by multiplicity (i.e. a double root counts twice, a
triple root three times etc.), then a polynomial of nth degree has n
roots.
The nth root of a complex number
We want to find the roots of the equation
rn=w,
where w is a given number. w may be complex, but the following procedure
is important even if w is real. The solution of the equation requires writing
w in polar form
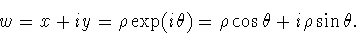
That is, if x and y are the real an imaginary parts of w, we want to
find  and
and  is such a way that
is such a way that
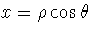 and
and 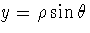 .
In other words,
.
In other words, 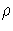 and
and 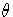 are
polar coordinates of the point (x,y) in the Cartesian plane.
are
polar coordinates of the point (x,y) in the Cartesian plane.
Examples:
1. w=1. In this case x=1 and y=0. We can choose 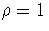 and
and 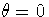 .
.
2. w=-1. Now x=-1 and y=0. We have 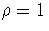 and
and 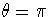 .
.
3. w=1+i. We have 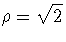 and
and 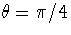 .
.
The point of using polar form is that it is very easy to take the nth root.
We find
![\begin{displaymath}
r=\sqrt[n]{w}=\sqrt[n]{\rho}\exp(i\theta/n).\end{displaymath}](img18.gif)
Since 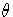 is an angle, it is not unique; it is determined only up to a
multiple of
is an angle, it is not unique; it is determined only up to a
multiple of 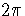 . That is, in the polar form of w, we could have written
. That is, in the polar form of w, we could have written
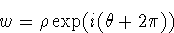
instead of 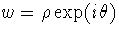 .
Although,
.
Although, 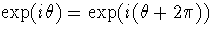 we have
we have
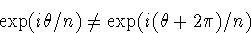
if n>1. To find all nth roots of w, you must consider the representations
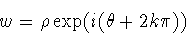
where k takes the integer values , 1, ..., n-1 (if you go further,
then k=n will give you the same as k=0). The nth roots of w are then
![\begin{displaymath}
\sqrt[n]{\rho}\exp(i(\theta+2k\pi)/n).\end{displaymath}](img25.gif)
Example:
r3=-1.
We put -1 into polar form
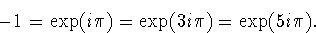
For the third roots, we find
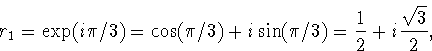
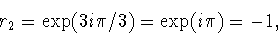
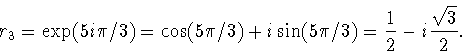
We could have found the same result from the factorization
r3+1=(r+1)(r2-r+1).
The quadratic formula gives
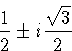
for the roots of the second factor.
WARNING
Beware of the difference between
(r+1)3=0
and
r3+1=0.
The first equation has a triple root at -1, the second has three different
roots: -1 and 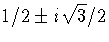 . In general, the equation rn=w
always has n DIFFERENT ROOTS. Be prepared for a whipping with the
cat of nine tails if you should ever say that the equation rn=w has an
n-fold root.
. In general, the equation rn=w
always has n DIFFERENT ROOTS. Be prepared for a whipping with the
cat of nine tails if you should ever say that the equation rn=w has an
n-fold root.



Next: About this document ...
Up: No Title
Previous: No Title
Michael Renardy
1998-03-04
![]()
![]()
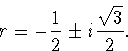
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
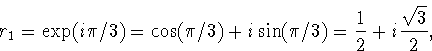
![]()