- We change to polar coordinates. Thus
x = rcosq,
y = rsinq, and
dA = r drdq. The circle
(x - 1)2 + y2 = 1
becomes
r2 - 2rcosq = 0, which simplifies to
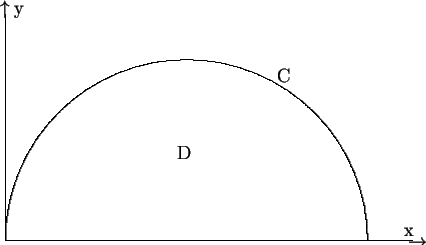
r = 2cosq. Also as one moves from (2, 0) to (0, 0)
on the semicircle C (see diagram
below),
q moves from 0 to
p/2. Therefore
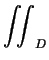 x3/(x2 + y2) dA x3/(x2 + y2) dA |
= 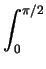 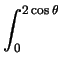 (r3cos3q/r2)rdrdq = (r3cos3q/r2)rdrdq = 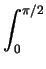 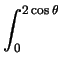 r2cos3q drdq r2cos3q drdq |
|
| |
= 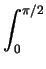 (8/3)cos6q dq = (8/3)cos6q dq = 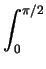 (1/3)(1 + cos 2q)3 dq (1/3)(1 + cos 2q)3 dq |
|
| |
= 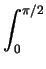 (1/3)(1 + 3cos22q) dq = 5p/12. (1/3)(1 + 3cos22q) dq = 5p/12. |
|
- Since r1r2 = 2, the roots r1, r2 will satisfy a quadratic
equation of the form
x2 + px + 2 = 0, where
p
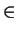 C.
Therefore we may factor
C.
Therefore we may factor
x4 - x3 + ax2 - 8x - 8 = (x2 + px + 2)(x2 + qx - 4)
where
q 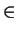 C. Equating the coefficients of x3 and
x, we obtain p + q = - 1 and 2q - 4p = - 8. Therefore p = 1 and q = - 2.
We conclude that a = - 4 and r1, r2 are the roots of x2 + x + 2, so
r1 and r2 are
(- 1±i
C. Equating the coefficients of x3 and
x, we obtain p + q = - 1 and 2q - 4p = - 8. Therefore p = 1 and q = - 2.
We conclude that a = - 4 and r1, r2 are the roots of x2 + x + 2, so
r1 and r2 are
(- 1±i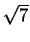 )/2.
)/2.
- The number of different combinations of possible flavors is the same
as the coefficient of x100 in
(1 + x + x2 + ...)4
This is the coefficient of x100 in
(1 - x)-4,
that is
103!/(3!100!) = 176851.
- We can represent the possible itineraries with a matrix. Thus we let
and let aij indicate the (i, j)th entry of A. Then for a one
day period, a11 is the number of itineraries from New York to New
York, a12 is the number of itineraries from New York to Los
Angeles, a21 is the number of itineraries from Los Angeles to New
York, and a22 is the number of itineraries
from Los Angeles to Los Angeles. The number of itineraries for
an n day period will be given
by An; in particular the (1, 1) entry of A100 will be the
number of itineraries starting and finishing at New York for a 100
day period.
To calculate A100, we diagonalize it.
Then the eigenvalues of A
are
1±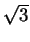 and the corresponding eigenvectors
(vectors
u satisfying
Au = lu
where
l = 1±
and the corresponding eigenvectors
(vectors
u satisfying
Au = lu
where
l = 1±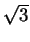 ) are
(±
) are
(±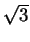 , 1).
Therefore if
, 1).
Therefore if
| | P = |
( |
| | 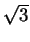 |
-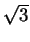 |
| | 1 |
1 |
|
) |
then
| | P-1AP = |
( |
| |
1 + 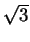 |
0 |
| | 0 |
1 - 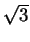 |
|
) |
Thus
| | A100 = |
P |
( |
| |
(1 + 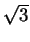 )100 )100 |
0 |
| | 0 |
(1 - 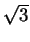 )100 )100 |
|
) |
P-1 |
We conclude that the (1, 1) entry of A100 is
((1 + 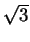 )100 + (1 -
)100 + (1 - 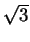 )100)/2, which is the number of
itineraries required.
)100)/2, which is the number of
itineraries required.
- For each city x in
S, let
Gx
 S
denote all the cities which you can travel from x
(this includes x). Clearly
Gx is well served and
| Gx|>3 (where | Gx| is the number
of cities in Gx). Choose x so that | Gx| is minimal. We need
to show that if
y, z
S
denote all the cities which you can travel from x
(this includes x). Clearly
Gx is well served and
| Gx|>3 (where | Gx| is the number
of cities in Gx). Choose x so that | Gx| is minimal. We need
to show that if
y, z 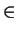 Gx, then one can travel from y
to z stopping only at cities in Gx; clearly we need only prove
this in the case z = x. So suppose by way of contradiction y
Gx, then one can travel from y
to z stopping only at cities in Gx; clearly we need only prove
this in the case z = x. So suppose by way of contradiction y 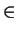 Gx and we cannot travel from y to x stopping only at cities in
Gx. Since
Gy
Gx and we cannot travel from y to x stopping only at cities in
Gx. Since
Gy 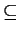 Gx and
x
Gx and
x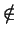 Gy, we have
| Gy| < | Gx|, contradicting the minimality of | Gx| and the result
follows.
Gy, we have
| Gy| < | Gx|, contradicting the minimality of | Gx| and the result
follows.
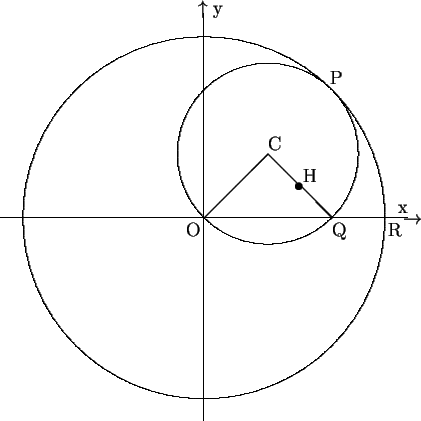
- Let O denote the center of the circle with radius 2cm., let
C denote the center of the disk with radius 1cm., and let H
denote the hole in the center of the disk. Choose axes so that the
origin is at O, and then let the initial position have C and H
on the positive x-axis with H furthest from O. The diagram
below is in general position (i.e. after the disk has been moved
round the inside of the circle).
Let P be the point of contact of the circle and the disk,
(so OCP will be a straight line), let Q be where CH meets the
circumference of the disk (on the x-axis, though we need to prove
that), and let R be where the circle meets the positive x-axis.
Since the arc lengths PQ and PR are equal and the circle has
twice the radius of that of the disk, we see that
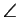 PCQ = 2
PCQ = 2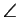 POR and it follows that Q does indeed lie on the
x-axis.
POR and it follows that Q does indeed lie on the
x-axis.
Let (a, b) be the coordinates of C. Then
a2 + b2 = 1 because
the disk has radius 1, and the coordinates of H are
(3a/2, b/2).
It follows that the curve H traces out is the ellipse
4x2 + 36y2 = 9. We now use the formula that the area of an ellipse
with axes of length 2p and 2q is
ppq. Here p = 3/2, q = 1/2, and we deduce that the area enclosed is
3p/4.
- Let
x = {x0, x1,..., xn}
 J. Then
J. Then
| Tx |
= |
LA({x0, x0 + x1, x0 + x1 + x2,...}) |
|
| |
= |
L({1 + x0, 1 + x0 + x1, 1 + x0 + x1 + x2,...}) |
|
| |
= |
{1, 1 + x0, 1 + x0 + x1, 1 + x0 + x1 + x2,...}. |
|
Therefore
T2y = T({1, 2, 3,...}) = {1, 1 + 1, 1 + 1 + 2, 1 + 1 + 2 + 3,...}. We deduce that
T2y = {1, 2, 4, 7, 11, 16, 22, 29,...} and
in general
(T2y)n = n(n + 1)/2 + 1.
Suppose
z = limi - > 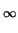 Tiy exists. Then
Tz = z, so 1 = z0,
1 + z0 = z1,
1 + z0 + z1 = z2,
1 + z0 + z1 + z2 = z3, etc. We now see that zn = 2n. To verify this, we use
induction on n, the case n = 0 already having been established.
Assume true for n; then
Tiy exists. Then
Tz = z, so 1 = z0,
1 + z0 = z1,
1 + z0 + z1 = z2,
1 + z0 + z1 + z2 = z3, etc. We now see that zn = 2n. To verify this, we use
induction on n, the case n = 0 already having been established.
Assume true for n; then
zn + 1 = 1 + z0 + z1 + ... + zn = 1 + 1 + 2 + ... + 2n = 2n + 1,
so the induction step is complete and the result is proven.
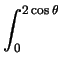 (r3cos3q/r2)rdrdq =
(r3cos3q/r2)rdrdq = 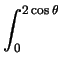 r2cos3q drdq
r2cos3q drdq
![]() and the corresponding eigenvectors
(vectors
u satisfying
Au = lu
where
l = 1±
and the corresponding eigenvectors
(vectors
u satisfying
Au = lu
where
l = 1±![]() ) are
(±
) are
(±![]() , 1).
Therefore if
, 1).
Therefore if
![]() )100 + (1 -
)100 + (1 - ![]() )100)/2, which is the number of
itineraries required.
)100)/2, which is the number of
itineraries required.

![]() Tiy exists. Then
Tz = z, so 1 = z0,
1 + z0 = z1,
1 + z0 + z1 = z2,
1 + z0 + z1 + z2 = z3, etc. We now see that zn = 2n. To verify this, we use
induction on n, the case n = 0 already having been established.
Assume true for n; then
Tiy exists. Then
Tz = z, so 1 = z0,
1 + z0 = z1,
1 + z0 + z1 = z2,
1 + z0 + z1 + z2 = z3, etc. We now see that zn = 2n. To verify this, we use
induction on n, the case n = 0 already having been established.
Assume true for n; then