15th VTRMC, 1993, Solutions

  1. We change the order of integration, so the integral becomes

    ∫01∫0√yey3/2 dxdy = ∫01y1/2ey3/2 = [2ey3/2/3]01 = (2e - 2)/3

    as required.

  2. Since f is continuous, ∫0xf (t) dt is a differentiable function of x, hence f is differentiable. Differentiating with respect to x, we obtain f'(x) = f (x). Therefore f (x) = Aex where A is a constant. Since f (0) = 0, we see that A = 0 and we conclude that f (x) is identically zero as required.

  3. From the definition, we see immediately that fn(1) = 1 for all n≥1. Taking logs, we get ln fn+1(x) = fn(x)ln x. Now differentiate both sides to obtain f'n+1(x)/fn+1(x) = fn'(x)ln x + fn(x)/x. Plugging in x = 1, we find that f'n+1(1)/fn+1(1) = fn(1) for all n≥1. It follows that f'n(1) = 1 for all n≥1. Differentiating

    f'n+1(x) = fn+1(x)fn'(x)ln x + fn+1(x)fn(x)/x,

    we obtain

    f''n+1(x) = f'n+1(x)fn'(x)ln x + fn+1(x)fn''(x)ln x + fn+1(x)fn'(x)/x + fn+1'(x)fn(x)/x + fn+1(x)fn'(x) - fn+1(x)fn(x)/x2.

    Plugging in x = 1 again, we obtain f''n(1) = 2 for all n≥2 as required.

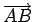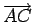  4. Suppose we have an equilateral triangle ABC with integer coordinates. Let u = $ \overrightarrow{AB}$ and v = $ \overrightarrow{AC}$. Then by expressing the cross product as a determinant, we see that |u×v| is an integer. Also |u|2 is an integer, and |u×v| = |u|2sin(π/3) because ∠BAC = π/3. We conclude that sin(π/3) = √3/2 is a rational number, which is not the case.

  5. For | x| < 1, we have the geometric series ∑n=0∞xn = 1/(1 - x). If we integrate term by term from 0 to x, we obtain ∑n=1∞xn/n = - ln(1 - x), which is also valid for | x| < 1. Now plug in x = 1/3: we obtain ∑n=1∞3-n/n = - ln(2/3) = ln 3 - ln 2.

  6. Suppose f is not bijective. Since f is surjective, this means that there is a point A0∈R2 such that at least two distinct points are mapped to A0 by f. Choose points B0, C0∈R2 such that A0, B0, C0 are not collinear. Now select points A, B, C∈R2 such that f (A) = A0, f (B) = B0 and f (C) = C0. Since f maps collinear points to collinear points, we see that A, B, C are not collinear. Now given two sets each with three non-collinear points, there is a bijective affine transformation (i.e. a linear map composed with a translation) sending the first set of points to the second set. This means that there are bijective affine transformations g, h : R2 --> R2 such that g(0, 0) = A, g(0, 1) = B, g(1, 0) = C, h(A0) = (0, 0), h(B0) = (0, 1), h(C0) = (1, 0). Then k : = hfg : R2 --> R2 fixes (0, 0),(0, 1),(1, 0), and has the property that if P, Q, R are collinear, the so are k(P), k(Q), k(R). Also there is a point (a, b)≠(0, 0) such that k(a, b) = (0, 0). We want to show that this situation cannot happen.

    Without loss of generality, we may assume that b≠ 0 Let ℓ denote the line joining (1, 0) to (0, b). Then k(ℓ) is contained in the x-axis. We claim that k maps the horizontal line through (0, 1) into itself. For if this was not the case, there would be a point with coordinates (c, d ) with d≠1 such that k(c, d )= (1, 1). Then if m was the line joining (c, d ) to (0, 1), we would have k(m) contained in the horizontal line through (0, 1). Since m intersects the x-axis and the x-axis is mapped into itself by k, this is not possible and so our claim is established. Now let ℓ meet this horizontal line at the point P. Then we have that k(P) is both on this horizontal line and also the x-axis, a contradiction and the result follows.

  7. The problem is equivalent to the following. Consider a grid in the xy-plane with horizontal lines at y = 2n + 1 and vertical lines at x = 2n + 1, where n is an arbitrary integer. A ball starts at the origin and travels in a straight line until it reaches a point of intersection of a horizontal line and a vertical line on the grid. Then we want to show that the distance dft travelled by the ball is not an integer number of feet. However d2 = (2m + 1)2 + (2n + 1)2 for some integers m, n and hence d2≡2 mod 4. Since d2 = 0 or 1 mod 4, we have a contradiction and the result is proven.

  8. The answer is 6; here is one way to get 6.


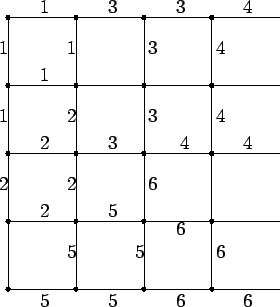
    \begin{picture}(60,67)(-6,-4) \matrixput(0,0)(15,0){4}(0,15){5}{\line(1,0){15}} ... ...,-4){6} \put(52,-4){6} \put(37,12){6} \put(46,7){6} \put(31,22){6} \end{picture}

    In this diagram, pieces of wire with the same corresponding number belong to the same logo. Also one needs to check that a welded point is not contained in more than one logo.

    On the other hand each logo has three welded points, yet the whole frame has only 20 welded points. Thus we cannot cut more than 20/3 logos and it follows that the maximum number of logos that can be cut is 6.



Peter Linnell 2008-05-21