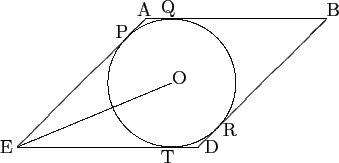
Suppose an+1 + 1 divides a2 + a2n, where n is a positive integer. Then an+1 + 1 divides an-1 - a2 and hence an+1 + 1 divides a4 + 1. Thus in particular n≤3. If n = 3, then an+1 +1 = a4 + 1 divides a2 + a2n = a2 + a6. If n = 1, then a2 + 1 divides 2a2 implies a2 + 1 divides 2, which is not possible. Finally if n = 2, we obtain a3 + 1 divides a2 + a4, so a3 + 1 divides a2 - a which again is not possible.
We conclude that if a > 1, then a2 + b2 is divisible by ab + 1 if and only if n = 3.
- (a)
-
f ([0, 1]) = [0, 1/3]∪[2/3, 1] f (f ([0, 1])) = [0, 1/9]∪[2/9, 3/9]∪[6/9, 7/9]∪[8/9, 1] f (f (f ([0, 1]))) = [0, 1/27]∪[2/27, 3/27]∪[6/27, 7, 27]∪[8/27, 9/27]∪ [18/27, 19/27] ∪[20/27, 21/27]∪[24/27, 25/27]∪[26/27, 1]
- (b)
- Let
T⊆R be a bounded set such that f (T) = T.
First note that T contains no negative numbers. Indeed if T
contains negative numbers, let
t0 = inft∈Tt and choose
t1∈T with
t1 < t0/3. Then
there is no
t∈T with
f (t) = t1.
Therefore we may assume that T contains no negative numbers. Now suppose 1/2∈T. Since (x + 2)/3 = 1/2 implies x = - 1/6, we see that 3/2∈T. Now let t2 = supt∈Tt and choose t3∈T such that t3 > (t2 + 2)/3. Since f (T) = T, we see that there exists s∈T such that f (s) > (t2 + 2)/3, which is not possible.
We conclude that there is no bounded subset T such that f (T) = T and 1/2∈T.