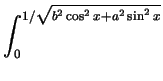 y dydx. We put this in more familiar form by replacing
x with
q and y with r to obtain
y dydx. We put this in more familiar form by replacing
x with
q and y with r to obtain
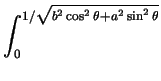 r drdq.
r drdq.
Now consider f (n) for n even. By switching the first letter between 2 and 3, we see that the number of words consisting of just 2's and 3's which have an even number of 2's is the same as the number of words with an odd number of 2's. Since the total number of words of length n is 2n, we deduce that A(n) = 2n - 1 when n is even. Therefore A(12) = 211 = 2048.
| f (n) | = f (n - 2) + ... + f (1) + 1 | |
| f (n - 1) | = f (n - 3) + ... + f (1) + 1 |
Therefore f (n) = f (n - 1) + f (n - 2). We now prove by induction that f (n) < 1.7n for all n. The result is certainly true for n = 1, 2. Suppose it is true for n - 2, n - 1, that is f (n - 2) < 1.7n - 2 and f (n - 1) < 1.7n - 1. Then
| ( |
|
) |
where x = 0 or 1. If x = 1, then the matrices X2n for n>1 are all different and members of T, which is not possible because | T| = 3. Therefore X2 = I and in particular I is in T. Thus we may label are members of T as X, Y, I, where I is the identity matrix and X2 = Y2 = I. Consider XYX. We have (XYX)(XYX) = XYX2YX = XY2X = X2 = I, so the eigenvalues of XYX are ±1. This means that XYX is another member of T, so must be one of X, Y, I. We now show that this is not possible. If XYX = X, then XYXXY = XXY = Y which yields X = Y. If XYX = I, then XXYXX = XX = I which yields Y = I. Neither of these is possible because X, Y, I are distinct. Finally if XYX = Y, then (XY)(XY) = I which shows that XY is also a member of T, so we must have XY = X, Y or I, and this is easily seen to be not the case.