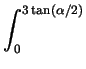 2 dx/(1 + x2) = 2tan-1(3tan(a/2)).
2 dx/(1 + x2) = 2tan-1(3tan(a/2)).
When t = 0, the initial condition tells us that x = 0, so x'(0) = 1 and we see that x(t) > 0 for small t. Suppose for some
positive t we have
x(t) ![]() 0. Then there is a least positive
number T such that x(T) = 0. Then x'(T) = 1, which leads to a
contradiction because x(t) > 0 for t < T. We deduce
that x(t) > 0 for all t.
0. Then there is a least positive
number T such that x(T) = 0. Then x'(T) = 1, which leads to a
contradiction because x(t) > 0 for t < T. We deduce
that x(t) > 0 for all t.
Now x' - 1 = x(x - 2t) and since x'(0) = 1, we see that x - 2t < 0 for small t. We deduce that for t sufficiently small, x(t) < t, consequently y(t) < 0 for small t. We now claim that y(t) < 0 for all positive t. If this is not the case, then there is a least positive number T such that y(T) = 0, and then we must have y'(S) = 0 for some S with 0 < S < T. But from y' = (y - t)(y + t) and (y + t) > 0, we would have to have y(S) = S, a contradiction because y(S) < 0. We deduce that x(t) < t for all positive t.
Now consider
x' = x(x - 2t) + 1. Note that we cannot have
x'(t)![]() 0 for all t, because then x - > 0 as
t - >
0 for all t, because then x - > 0 as
t - > ![]() which is
clearly impossible, consequently x' takes on negative values.
Next we have
x'' = 2(xx' - tx' - x),
so if x'(t) = 0, we see that
x''(t) < 0. We deduce that if
x'(T) < 0, then x'(t) < 0 for all t > T. Thus there is a
positive number T such that x'(t) < 0 for all t > T. Now
differentiate again to obtain
x''' = 2(xx'' + x'x' - tx'' - 2x'). Then we see that if
x''(t) = 0 and t > T,
then
x'''(t) > 0, consequently there is a positive number S > T
such that either
x''(t) < 0 for all t > S or
x''(t) > 0 for all
t > S. We deduce that x'(t) is monotonic increasing or
decreasing for t > S and hence
limt - >
which is
clearly impossible, consequently x' takes on negative values.
Next we have
x'' = 2(xx' - tx' - x),
so if x'(t) = 0, we see that
x''(t) < 0. We deduce that if
x'(T) < 0, then x'(t) < 0 for all t > T. Thus there is a
positive number T such that x'(t) < 0 for all t > T. Now
differentiate again to obtain
x''' = 2(xx'' + x'x' - tx'' - 2x'). Then we see that if
x''(t) = 0 and t > T,
then
x'''(t) > 0, consequently there is a positive number S > T
such that either
x''(t) < 0 for all t > S or
x''(t) > 0 for all
t > S. We deduce that x'(t) is monotonic increasing or
decreasing for t > S and hence
limt - > ![]() x'(t) exists
(possibly infinite).
x'(t) exists
(possibly infinite).
We now have x'(t) is monotonic and negative for t > S, yet x(t) > 0 for all t > S. We deduce that
limt - > ![]() x'(t) = 0
and the result follows.
x'(t) = 0
and the result follows.
| l22 | = | (l - x)2 + y2 + 2(l - x)ycosq | |
| l12 | = | x2 + y2 - 2xycosq |
Subtracting the second equation from the first we obtain
Suppose this is not the case. Let
bn = Sm = 1nam(2/9)m. If
a = 2/3 or ![]() , then there exists a
positive integer N such that bN < 1/3 and
bN + 1
, then there exists a
positive integer N such that bN < 1/3 and
bN + 1![]() 1/3.
Then the same argument as above gives
1/3.
Then the same argument as above gives