21st Annual
Virginia Tech Regional Mathematics Contest
From 8:30a.m. to 11:00a.m., October 30, 1999
Fill out the individual registration form
- Let
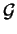 be the set of all continuous functions
f :
be the set of all continuous functions
f : 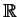 - >
- > 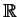 , satisfying the following properties.
, satisfying the following properties.
- (i)
-
f (x) = f (x + 1) for all x,
- (ii)
-
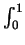 f (x) dx = 1999.
f (x) dx = 1999.
Show that there is a number
a such that
a = 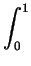
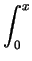 f (x + y) dydx
for all
f
f (x + y) dydx
for all
f 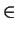
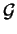 .
.
- Suppose that
f :
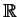 - >
- > 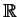 is infinitely
differentiable and satisfies both of the following properties.
is infinitely
differentiable and satisfies both of the following properties.
- (i)
- f (1) = 2,
- (ii)
- If
a,b are real numbers satisfying
a2 + b2 = 1, then
f (ax)f (bx) = f (x) for all x.
Find f (x). Guesswork will not be accepted.
- Let
e, M be positive real numbers, and let
A1, A2,...
be a sequence of matrices such that for all n,
- (i)
- An is an n X n matrix with integer entries,
- (ii)
- The sum of the absolute values of the entries in each row of
An is at most M.
If
d is a positive real number, let
en(d) denote the
number of nonzero eigenvalues of An which have absolute value less
that
d. (Some eigenvalues can be complex numbers.) Prove
that one can choose
d > 0 so that
en(d)/n < e
for all n.
- A rectangular box has sides of length 3, 4, 5. Find the volume of
the region consisting of all points that are within distance 1 of at
least one of the sides.
- Let
f :
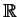 + - >
+ - > 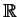 + be a function from the
set of positive real numbers to the same set satisfying
f (f (x)) = x
for all positive x. Suppose that f is infinitely differentiable
for all positive X, and that
f (a)
+ be a function from the
set of positive real numbers to the same set satisfying
f (f (x)) = x
for all positive x. Suppose that f is infinitely differentiable
for all positive X, and that
f (a)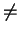 a for some positive a.
Prove that
a for some positive a.
Prove that
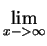 f (x) = 0.
f (x) = 0.
- A set
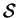 of distinct positive integers has property
ND if no element x of
of distinct positive integers has property
ND if no element x of
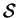 divides the sum of
the integers in any subset of
S\{x}. Here
divides the sum of
the integers in any subset of
S\{x}. Here
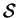 \{x} means the set that remains after x is removed
from
\{x} means the set that remains after x is removed
from
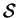 .
.
- (i)
- Find the smallest positive integer n such that {3, 4, n} has
property ND.
- (ii)
- If n is the number found in (i), prove that no set
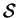 with property ND has {3, 4, n} as a proper
subset.
with property ND has {3, 4, n} as a proper
subset.
Peter Linnell
2000-09-08
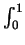 f (x) dx = 1999.
f (x) dx = 1999.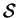 with property ND has {3, 4, n} as a proper
subset.
with property ND has {3, 4, n} as a proper
subset.