20th Annual
Virginia Tech Regional Mathematics Contest
From 8:30a.m. to 11:00a.m., October 31, 1998
Fill out the individual registration form
- Let
f (x, y) = ln(1 - x2 - y2) - 1/(y - x)2 with domain
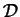 = {(x, y) | x
= {(x, y) | x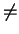 y, x2 + y2 < 1}. Find the
maximum value M of f (x, y) over
y, x2 + y2 < 1}. Find the
maximum value M of f (x, y) over
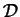 . You have to show
that
M
. You have to show
that
M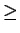 f (x, y) for every
(x, y)
f (x, y) for every
(x, y) 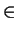
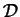 . Here
ln(·) is the natural logarithm function.
. Here
ln(·) is the natural logarithm function.
- The radius of the base of a right circular cone is 1. The
vertex of the cone is V, and P is a point on the circumference of
the base. The length of PV is 6 and the midpoint of PV is M.
A piece of string is attached to M and wound tightly twice round the
cone finishing at P. What is the length of the string?
- Find the volume of the region which is common to the interiors of the
three circular cylinders
y2 + z2 = 1,
z2 + x2 = 1 and
x2 + y2 = 1.
- Let ABC be a triangle and let P be a point on AB. Suppose
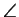 BAC = 70o,
BAC = 70o,
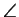 APC = 60o,
AC =
APC = 60o,
AC = 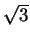 and PB = 1.
Prove that ABC is an isosceles triangle.
and PB = 1.
Prove that ABC is an isosceles triangle.
- Let an be sequence of positive numbers (
n = 1, 2,..., an
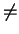 0 for all n), and let
bn = (a1 + ... + an)/n, the
average of the first n numbers of the sequence. Suppose
S
0 for all n), and let
bn = (a1 + ... + an)/n, the
average of the first n numbers of the sequence. Suppose
S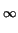 n = 11/an
is a convergent series. Prove that
Sn = 1
n = 11/an
is a convergent series. Prove that
Sn = 1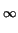 1/bn is also a convergent series.
1/bn is also a convergent series.
- Ten cats are sitting on ten fence posts, numbered 1 through 10 in
clockwise order and encircling a pumpkin patch. The cat on post #1 is white and the other nine cats are black. At 9:45p.m. the
cats begin a strange sort of dance. They jump from post to post
according to the following two rules, applied in alternation at one
second intervals. Rule 1: each cat jumps clockwise to the next
post. Rule 2: all pairs of cats whose post numbers have a product
that is 1 greater than a multiple of 11 exchange places. At
10p.m., just as the Great Pumpkin rises out of the pumpkin patch,
the dance stops abruptly and the cats look on in awe. If the first
jump takes place according to Rule 1 at 9:45:01, and the last jump
occurs at 10:00:00, on which post is the white cat sitting when the
dance stops? (The first few jumps take the white cat from post 1 to
posts 2,6,7, ...)
Peter Linnell
2000-09-08