19th Annual
Virginia Tech Regional Mathematics Contest
From 8:30a.m. to 11:00a.m., November 1, 1997
Fill out the individual registration form
- Evaluate
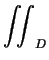 x3/(x2 + y2) dA, where D is the half disk given by
(x - 1)2 + y2
x3/(x2 + y2) dA, where D is the half disk given by
(x - 1)2 + y2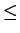 1, y
1, y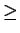 0.
0.
- Suppose that
r1
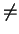 r2 and
r1r2 = 2. If r1 and
r2 are roots of
r2 and
r1r2 = 2. If r1 and
r2 are roots of
x4 - x3 + ax2 - 8x - 8 = 0,
find r1, r2 and a. (Do not assume that they are real numbers.)
- Suppose that you are in charge of taking ice cream orders for a class
of 100 students. If each student orders exactly one flavor from
Vanilla, Strawberry, Chocolate and Pecan, how many different
combinations of flavors are possible for the 100 orders you are
taking. Here are some examples of possible combinations. You do not
distinguish between individual students.
- (i)
- V = 30, S = 20, C = 40, P = 10.
- (ii)
- V = 80, S = 0, C = 20, P = 0.
- (iii)
- V = 0, S = 0, C = 0, P = 100.
- A business man works in New York and Los Angeles. If he is in New
York, each day he has four options; to remain in New York, or to fly
to Los Angeles by either the 8:00a.m., 1:00p.m. or 6:00p.m. flight. On the other hand if he is in Los Angeles, he has only two
options; to remain in Los Angeles, or to fly to New York by the
8:00a.m. flight. In a 100 day period he has to be in New York
both at the beginning of the first day of the period, and at the end
of the last day of the period. How many different possible
itineraries does the business man have for the 100 day period (for
example if it was for a 2 day period rather than a 100 day period,
the answer would be 4)?
- The VTRC bus company serves cities in the USA. A subset
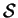 of the cities is called well-served if it has at least
three cities and from every city
of the cities is called well-served if it has at least
three cities and from every city
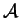 in
in
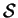 ,
one can take a nonstop VTRC bus to at least two different other
cities
,
one can take a nonstop VTRC bus to at least two different other
cities
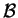 and
and
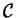 in
in
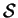 (though
there is not necessarily a nonstop VTRC bus from
(though
there is not necessarily a nonstop VTRC bus from
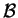 to
to
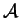 or from
or from
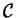 to
to
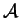 ). Suppose
there is a well-served subset
). Suppose
there is a well-served subset
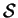 . Prove that there is a
well-served subset
. Prove that there is a
well-served subset
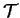 such that for any two cities
such that for any two cities
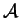 ,
,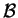 in
in
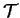 , one can travel by
VTRC bus from
, one can travel by
VTRC bus from
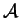 to
to
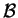 , stopping only at
cities in
, stopping only at
cities in
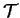 .
.
- A disk of radius 1cm. has a small hole at a point half way
between the center and the circumference. The disk is lying inside a
circle of radius 2cm. A pen is put through the hole in the disk,
and then the disk is moved once round the inside of the circle,
keeping the disk in contact with the circle without slipping, so the
pen draws a curve. What is the area enclosed by the curve?
- Let
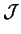 be the set of all sequences of real numbers,
and let A, L and P be three mappings from
be the set of all sequences of real numbers,
and let A, L and P be three mappings from
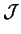 to
to
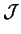 defined as follows. If
x = {xn} = {x0, x1, x2,...}
defined as follows. If
x = {xn} = {x0, x1, x2,...} 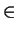
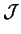 , then
, then
| Ax = {xn + 1} |
= {x0 + 1, x1 + 1, x2 + 1,...}, |
|
| Lx |
= {1, x0, x1, x2,...}, |
|
| Px |
= {Snk = 0xk}. |
|
Finally, define the composite mapping T on
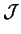 by
Tx = LoAoPx. In the following, let
y = {1, 1, 1,...}.
by
Tx = LoAoPx. In the following, let
y = {1, 1, 1,...}.
- (a)
- Write down T2y, giving the first eight terms of the
sequence and a closed formula for the n-th term.
- (b)
- Assuming that
z = {zn} = limi - >
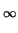 Tiy exists, conjecture the general form for zn, and prove your
conjecture.
Tiy exists, conjecture the general form for zn, and prove your
conjecture.
Peter Linnell
2000-09-08
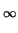 Tiy exists, conjecture the general form for zn, and prove your
conjecture.
Tiy exists, conjecture the general form for zn, and prove your
conjecture.