18th Annual
Virginia Tech Regional Mathematics Contest
From 9:00a.m. to 11:30a.m., October 26, 1996
Fill out the individual registration form
- Evaluate
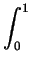
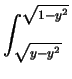 xe(x4 + 2x2y2 + y4) dxdy.
xe(x4 + 2x2y2 + y4) dxdy.
- For each rational number r, define f (r) to be the smallest
positive integer n such that r = m/n for some integer m, and
denote by P(r) the point in the (x, y) plane with coordinates
P(r) = (r, 1/f (r)). Find a necessary and sufficient condition that,
given two rational numbers r1 and r2 such that
0 < r1 < r2 < 1,
P((r1f (r1) + r2f (r2))/(f (r1) + f (r2)))
will be the point of intersection of the line joining (r1, 0) and
P(r2) with the line joining P(r1) and (r2, 0).
- Solve the differential equation
yy = edy/dx
with the initial condition y = e when x = 1.
- Let f (x) be a twice continuously differentiable in the
interval
(0,
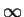 ). If
). If
lim
x - > 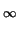
(
x2f''(
x) + 4
xf'(
x) + 2
f (
x)) = 1,
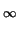 f (x) and
limx - >
f (x) and
limx - > 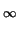 xf'(x). Do
not assume any special form of f (x). Hint: use
l'Hôpital's rule.
xf'(x). Do
not assume any special form of f (x). Hint: use
l'Hôpital's rule.
- Let ai,
i = 1, 2, 3, 4, be real numbers such that
a1 + a2 + a3 + a4 = 0. Show that for arbitrary real numbers bi, i = 1, 2, 3,
the equation
a1 + b1x + 3a2x2 + b2x3 + 5a3x4 + b3x5 + 7a4x6 = 0
has at least one real root which is on the interval
-1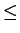 x
x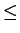 1.
1.
- There are 2n balls in the plane such that no three balls are
on the same line and such that no two balls touch each other. n
balls are red and the other n balls are green. Show that there is
at least one way to draw n line segments by connecting each ball to
a unique different colored ball so that no two line segments
intersect.
- Let us define
| fn, 0(x) |
= x + (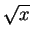 )/n )/n |
|
forx > 0, n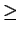 1, 1, |
|
| fn, j + 1(x) |
= fn, 0(fn, j(x)), |
|
j = 0, 1,..., n - 1. |
|
Find
limn - > 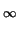 fn, n(x) for x > 0.
fn, n(x) for x > 0.
Peter Linnell
2000-09-08
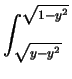 xe(x4 + 2x2y2 + y4) dxdy.
xe(x4 + 2x2y2 + y4) dxdy.
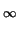 (x2f''(x) + 4xf'(x) + 2f (x)) = 1,
(x2f''(x) + 4xf'(x) + 2f (x)) = 1,