16th Annual
Virginia Tech Regional Mathematics Contest
From 9:00a.m. to 11:30a.m., October 29, 1994
Fill out the individual registration form
- Evaluate
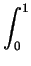
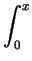
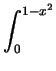 e(1 - z)2 dzdydx.
e(1 - z)2 dzdydx.
- Let f be continuous real function, strictly increasing in an
interval [0, a] such that f (0) = 0. Let g be the inverse of
f, i.e.,
g(f (x)) = x for all x in [0, a]. Show that for
0
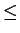 x
x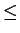 a,
0
a,
0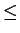 y
y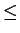 f (a), we have
f (a), we have
- Find all continuously differentiable solutions f (x) for
f (
x)
2 =
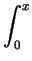
(
f (
t)
2 -
f (
t)
4 + (
f'(
t))
2) d
t + 100
where
f (0)2 = 100.
- Consider the polynomial equation
ax4 + bx3 + x2 + bx + a = 0, where a and b are real numbers, and a > 1/2. Find the
maximum possible value of a + b for which there is at least one
positive real root of the above equation.
- Let
f :
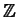 X
X
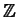 - >
- > 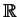 be a function which satisfies
f (0, 0) = 1 and
be a function which satisfies
f (0, 0) = 1 and
f (m, n) + f (m + 1, n) + f (m, n + 1) + f (m + 1, n + 1) = 0
for all
m, n 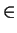
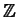 (where
(where
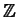 and
and
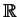 denote the set of all integers and all real numbers, respectively).
Prove that
| f (m, n)|
denote the set of all integers and all real numbers, respectively).
Prove that
| f (m, n)|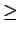 1/3, for infinitely many pairs of integers
(m, n).
1/3, for infinitely many pairs of integers
(m, n).
- Let A be an n X n matrix and let
a be an
n-dimensional vector such that
Aa = a. Suppose that
all the entries of A and
a are positive real numbers. Prove
that
a is the only linearly independent eigenvector of A
corresponding to the eigenvalue 1. Hint: if
b is another
eigenvector, consider the minimum of
ai/|bi|,
i = 1,..., n, where the
ai's and
bi's are the components
of
a and
b, respectively.
- Define f (1) = 1 and
f (n + 1) = 2
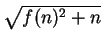 for n
for n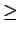 1. If N
1. If N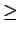 1 is an integer, find
Sn = 1Nf (n)2.
1 is an integer, find
Sn = 1Nf (n)2.
- Let a sequence
{xn}n = 0
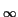 of rational numbers be
defined by x0 = 10, x1 = 29 and
xn + 2 = 19xn + 1/(94xn) for n
of rational numbers be
defined by x0 = 10, x1 = 29 and
xn + 2 = 19xn + 1/(94xn) for n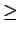 0. Find
Sn = 0
0. Find
Sn = 0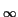 x6n/2n.
x6n/2n.
Peter Linnell
2000-09-08
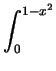 e(1 - z)2 dzdydx.
e(1 - z)2 dzdydx.
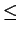
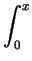 f (t) dt +
f (t) dt + 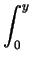 g(t) dt.
g(t) dt.
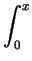 (f (t)2 - f (t)4 + (f'(t))2) dt + 100
(f (t)2 - f (t)4 + (f'(t))2) dt + 100
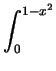 e(1 - z)2 dzdydx.
e(1 - z)2 dzdydx.