15th Annual
Virginia Tech Regional Mathematics Contest
From 9:00a.m. to 11:30a.m., October 30, 1993

Fill out the individual registration form

  1. Prove that ∫01∫x21ey3/2 dydx = (2e - 2)/3.

  2. Prove that if f : R --> R is continuous and f (x) = ∫0xf (t) dt, then f (x) is identically zero.

  3. Let f1(x) = x and fn+1(x) = xfn(x), for n = 1, 2.... Prove that fn'(1) = 1 and fn''(1) = 2, for all n≥2.

  4. Prove that a triangle in the plane whose vertices have integer coordinates cannot be equilateral.

  5. Find ∑n=1∞3-n/n.

  6. Let f : R2 --> R2 be a surjective map with the property that if the points A, B and C are collinear, then so are f (A), f (B) and f (C). Prove that f is bijective.

  7. On a small square billiard table with sides of length 2ft., a ball is played from the center and after rebounding off the sides several times, goes into a cup at one of the corners. Prove that the total distance travelled by the ball is not an integer number of feet.


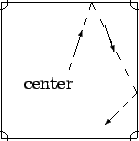
    \begin{picture}(33,33) \put(0,0){\line(1,0){30}} \put(0,0){\line(0,1){30}} \put(... ...3){2}} \put(23,25){\vector(1,-3){2}} \put(25,5){\vector(-1,-1){2}} \end{picture}

  8. A popular Virginia Tech logo looks something like


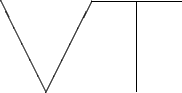
    \begin{picture}(60,21) \put(10,0){\line(-1,2){10}} \put(10,0){\line(1,2){10}} \put(20,20){\line(1,0){20}} \put(30,0){\line(0,1){20}} \end{picture}

    Suppose that wire-frame copies of this logo are constructed of 5 equal pieces of wire welded at three places as shown:


    \begin{picture}(68,21) \put(9,2){\line(-1,2){9}} \put(9,2){\line(1,2){9}} \put(1... ...,2){\circle*{1}} \put(18,20){\circle*{1}} \put(38,20){\circle*{1}} \end{picture}

    If bending is allowed, but no re-welding, show clearly how to cut the maximum possible number of ready-made copies of such a logo from the piece of welded wire mesh shown. Also, prove that no larger number is possible.


    \begin{picture}(60,61) \matrixput(0,0)(15,0){4}(0,15){5}{\line(1,0){15}} \matrixput(0,0)(15,0){4}(0,15){4}{\line(0,1){15}} \end{picture}



Peter Linnell 2007-06-15