14th Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to 12:00 noon, October 31, 1992
Fill out the individual registration form
- Find the inflection point of the graph of
F(x) = ∫0x3et2 dt, for
x∈R.
- Assume that
x1 > y1 > 0 and
y2 > x2 > 0. Find a
formula for the shortest length l of a planar path that goes from
(x1, y1) to (x2, y2) and that touches both the x-axis and the
y-axis. Justify your answer.
- Let fn(x) be defined recursively by
f0(x) = x, f1(x) = f (x), fn+1(x) = f (fn(x)), for n≥0,
where
f (x) = 1 + sin(x - 1).
- (i)
- Show that there is a unique point x0 such that
f2(x0) = x0.
- (ii)
- Find
∑n=0∞fn(x0)/3n
with the above x0.
- Let
{tn}n=1∞ be a sequence of positive numbers
such that t1 = 1 and
tn+12 = 1 + tn, for
n≥1. Show
that tn is increasing in n and find
limn--> ∞tn.
- Let
Find A100. You have to find all four entries.
- Let p(x) be the polynomial
p(x) = x3 + ax2 + bx + c.
Show that if p(r) = 0, then
p(x)/(x - r) - 2p(x + 1)/(x + 1 - r) + p(x + 2)/(x + 2 - r) = 2
for all x except x = r, r - 1 and r - 2.
- Find
limn--> ∞(2 log 2 + 3 log 3 + ... + n log n)/(n2log n).
- Some goblins, N in number, are standing in a row while
``trick-or-treat"ing. Each goblin is at all times either 2' tall
or 3' tall, but can change spontaneously from one of these two
heights to the other at will. While lined up in such a row, a goblin
is called a Local Giant Goblin (LGG) if he/she/it is not
standing beside a taller goblin. Let G(N) be the total of all
occurrences of LGG's as the row of N goblins transmogrifies
through all possible distinct configurations, where height is the
only distinguishing characteristic. As an example, with N = 2, the
distinct configurations are
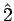
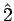 , 2
, 2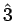 ,
,
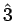 2,
2,
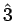
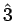 , where a cap indicates an LGG. Thus
G(2) = 6.
, where a cap indicates an LGG. Thus
G(2) = 6.
- (i)
- Find G(3) and G(4).
- (ii)
- Find, with proof, the general formula for G(N),
N = 1, 2, 3,....
Peter Linnell
2008-05-21