13th Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to 12:00 noon, October 19, 1991

Fill out the individual registration form

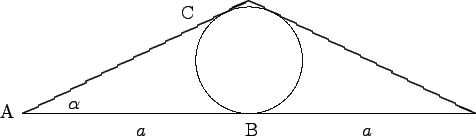
  1. An isosceles triangle with an inscribed circle is labeled as shown in the figure. Find an expression, in terms of the angle α and the length a, for the area of the curvilinear triangle bounded by sides AB and AC and the arc BC.


    \begin{picture}(108,29)(-3,-3) \put(0,0){\line(1,0){100}} \put(0,0){\line(2,1){5... ...$a$} \put(75,-5){$a$} \put(49,-5){B} \put(35,21){C} \put(-5,-1){A} \end{picture}

  2. Find all differentiable functions f which satisfy f (x)3 = ∫0xf (t)2 dt for all real x.

  3. Prove that if α is a real root of (1 - x2)(1 + x + x2 + ... + xn) - x = 0 which lies in (0, 1), with n = 1, 2,..., then α is also a root of (1 - x2)(1 + x + x2 + ... + xn+1) - 1 = 0.

  4. Prove that if x > 0 and n > 0, where x is real and n is an integer, then

    xn/((x + 1)n+1)≤nn/((n + 1)n+1).

  5. Let f (x) = x5 -5x3 + 4x. In each part (i)-(iv), prove or disprove that there exists a real number c for which f (x) - c = 0 has a root of multiplicity

    (i) one,    (ii) two,    (iii) three,    (iv) four.

  6. Let a0 = 1 and for n > 0, let an be defined by

    an = - ∑k=1nan-k/k!.

    Prove that an = (- 1)n/n!, for n = 0, 1, 2,....

  7. A and B play the following money game, where an and bn denote the amount of holdings of A and B, respectively, after the nth round. At each round a player pays one-half his holdings to the bank, then receives one dollar from the bank if the other player had less than c dollars at the end of the previous round. If a0 = .5 and b0 = 0, describe the behavior of an and bn when n is large, for

    (i) c = 1.24     and     (ii) c = 1.26.

  8. Mathematical National Park has a collection of trails. There are designated campsites along the trails, including a campsite at each intersection of trails. The rangers call each stretch of trail between adjacent campsites a ``segment". The trails have been laid out so that it is possible to take a hike that starts at any campsite, covers each segment exactly once, and ends at the beginning campsite. Prove that it is possible to plan a collection C of hikes with all of the following properties:
    (i)
    Each segment is covered exactly once in one hike h∈C and never in any of the other hikes of C.

    (ii)
    Each h∈C has a base campsite that is its beginning and end, but which is never passed in the middle of the hike. (Different hikes of C may have different base campsites.)

    (iii)
    Except for its base campsite at beginning and end, no hike in C passes any campsite more than once.



Peter Linnell 2009-06-24