11th Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to noon October 21, 1989

Fill out the individual registration form

1. A square of side a is inscribed in a triangle of base b and height h as shown. Prove that the area of the square cannot exceed one-half the area of the triangle.

   
   
   

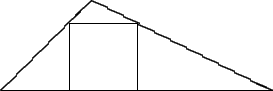
2. Let A be a 3×3 matrix in which each element is either 0 or 1 but is otherwise arbitrary.

   (a)

   Prove that det(A) cannot be 3 or -3.

   (b)

   Find all possible values of det(A) and prove your result.

3. The system of equations
   

   a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁

   a₂₁x₁ + a₂₂x₂ + a₂₃x₃ = b₂

   a₃₁x₁ + a₃₂x₂ + a₃₃x₃ = b₃

   
   has the solution x₁ = -1, x₂ = 3, x₃ = 2 when b₁ = 1, b₂ = 0, b₃ = 1 and it has the solution x₁ = 2, x = -2, x₃ = 1 when b₁ = 0, b₂ = - 1, b₃ = 1. Find a solution of the system when b₁ = 2, b₂ = - 1, b₃ = 3.

4. Let a, b, c, d be distinct integers such that the equation
   (x - a)(x - b)(x - c)(x - d )- 9 = 0
   has an integer root r. Show that 4r = a + b + c + d. (This is essentially a problem from the 1947 Putnam examination.)

5. (i)

   Prove that f₀(x) = 1 + x + x² + x³ + x⁴ has no real zero.

   (ii)

   Prove that, for every integer n≥ 0, f_n(x) = 1 + 2^-nx + 3^-nx² +4^-nx³ +5^-nx⁴ has no real zero. (Hint: consider (d /dx)(xf_n(x)).)

6. Let g be defined on (1,∞) by g(x) = x/(x - 1), and let f^k(x) be defined by f⁰(x) = x and for k > 0, f^k(x) = g(f^k-1(x)). Evaluate ∑_k=0^∞2^-kf^k(x) in the form (ax² + bx + c)/(dx + e).

7. Three farmers sell chickens at a market. One has 10 chickens, another has 16, and the third has 26. Each farmer sells at least one, but not all, of his chickens before noon, all farmers selling at the same price per chicken. Later in the day each sells his remaining chickens, all again selling at the same reduced price. If each farmer received a total of $35 from the sale of his chickens, what was the selling price before noon and the selling price after noon? (From ``Math Can Be Fun" by Ya Perelman.)

8. The integer sequence {a₀, a₁,..., a_n-1} is such that, for each i ( 0≤i≤n - 1), a_i is the number of i's in the sequence. (Thus for n = 4 we might have the sequence {1, 2, 1, 0}.)

   (a)

   Prove that, if n≥7, such a sequence is a unique.

   (b)

   Find such a sequence for n = 7.

   Hint: show that the sum of all the terms is n, and that there are n - a₀ - 1 nonzero terms other than a₀ which sum to n - a₀. (This problem is slightly modified from one on the Cambridge Men's Colleges Joint Awards and Entrance Examination, 24 November 1970.)