10th Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to 12:00 noon, October 22, 1988
Fill out the individual registration form
- A circle C of radius r is circumscribed by a parallelogram S.
Let
q denote one of the interior angles of S, with
0 < q
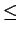 p/2. Calculate the area of S as a function of r
and
q.
p/2. Calculate the area of S as a function of r
and
q.
- A man goes into a bank to cash a check. The teller mistakenly
reverses the amounts and gives the man cents for dollars and dollars
for cents. (Example: if the check was for $5.10, the man was given
$10.05.). After spending five cents, the man finds that he still
has twice as much as the original check amount. What was the
original check amount? Find all possible solutions.
- Find the general solution of
y(x) +
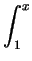 y(t) dt = x2.
y(t) dt = x2.
- Let a be a positive integer. Find all positive integers n such
that b = an satisfies the condition that a2 + b2 is divisible
by ab + 1.
- Let f be differentiable on [0, 1] and let
f (a) = 0 and
f (x0) = - .0001 for some
a and
x0
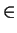 (0, 1). Also let
| f'(x)|
(0, 1). Also let
| f'(x)|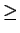 2 on [0, 1]. Find the smallest upper bound on
|a - x0| for all such functions.
2 on [0, 1]. Find the smallest upper bound on
|a - x0| for all such functions.
- Find positive real numbers a and b such that
f (x) = ax - bx3
has four extrema on [- 1, 1], at each of which
| f (x)| = 1.
- For any set S of real numbers define a new set f (S) by
f (S) = {x/3 | x
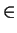 S}
S} 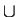 {(x + 2)/3 | x
{(x + 2)/3 | x 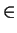 S}.
S}.
- (a)
- Sketch, carefully, the set
f (f (f (I))), where I is the interval
[0, 1].
- (b)
- If T is a bounded set such that f (T) = T, determine, with
proof, whether T can contain 1/2.
- Let T(n) be the number of incongruent triangles with integral sides
and perimeter n
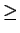 6. Prove that
T(n) = T(n - 3) if n is even,
or disprove by a counterexample. (Note: two triangles are
congruent if there is a one-to-one correspondence between the
sides of the two triangles such that corresponding sides have the
same length.)
6. Prove that
T(n) = T(n - 3) if n is even,
or disprove by a counterexample. (Note: two triangles are
congruent if there is a one-to-one correspondence between the
sides of the two triangles such that corresponding sides have the
same length.)
Peter Linnell
2001-08-12