9th Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to 12:00 noon, October 31, 1987
Fill out the individual registration form
- A path zig-zags from (1, 0) to (0, 0) along line segments
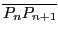 , where P0 is (1, 0) and Pn is
(2-n,(- 2)-n), for n > 0. Find the length of the path.
, where P0 is (1, 0) and Pn is
(2-n,(- 2)-n), for n > 0. Find the length of the path.
- A triangle with sides of lengths a, b, and c is partitioned
into two smaller triangles by the line which is perpendicular to the
side of length c and passes through the vertex opposite that side.
Find integers a < b < c such that each of the two smaller
triangles is similar to the original triangle and has sides of
integer lengths.
- Let
a1, a2,..., an be an arbitrary rearrangement of
1, 2,..., n. Prove that if n is odd, then
(a1 -1)(a2 -2)...(an - n) is even.
- Let p(x) be given by
p(x) = a0 + a1x + a2x2 + ... + anxn
and let
| p(x)|≤| x| on [- 1, 1].
(a) Evaluate a0. (b) Prove that
| a1|≤1.
- A sequence of integers
{n1, n2,...} is defined as follows:
n1 is assigned arbitrarily and, for k > 1,
nk = ∑j=1j=k-1z(nj),
where z(n) is the number of 0's in the binary representation of n
(each representation should have a leading digit of 1 except for zero
which has the representation 0). An example, with n1 = 9, is
{9, 2, 3, 3, 3,...}, or in binary,
{1001, 10, 11, 11, 11,...}.
- (a)
- Find n1 so hat
limk-> ∞nk = 31, and calculate
n2, n3,..., n10.
- (b)
- Prove that, for every choice of n1, the sequence {nk}
converges.
- A sequence of polynomials is given by
pn(x) = an+2x2 + an+1x - an, for
n≥ 0, where
a0 = a1 = 1 and, for
n≥ 0,
an+2 = an+1 + an. Denote by rn and sn the roots of
pn(x) = 0, with
rn≤sn. Find
limn-> ∞rn and
limn-> ∞sn.
- Let
A = {aij} and
B = {bij} be
n×n matrices
such that A-1 exists. Define
A(t) = {aij(t)} and
B(t) = {bij(t)} by
aij(t) = aij for i < n,
anj(t) = tanj,
bij(t) = bij for i < n, and
bnj(t) = tbnj.
For example, if
then
Prove that
A(t)-1B(t) = A-1B for t > 0 and any n. (Partial
credit will be given for verifying the result for n = 3.)
- On Halloween, a black cat and a witch encounter each other near a
large mirror positioned along the y-axis. The witch is
invisible except by reflection in the mirror. At t = 0, the
cat is at (10, 10) and the witch is at (10, 0). For
t≥ 0, the
witch moves toward the cat at a speed numerically equal to their
distance of separation and the cat moves toward the apparent position
of the witch, as seen by reflection, at a speed numerically equal to
their reflected distance of separation. Denote by
(u(t), v(t)) the
position of the cat and by
(x(t), y(t)) the position of the witch.
- (a)
- Set up the equations of motion of the cat and the witch for
t≥ 0.
- (b)
- Solve for x(t) and u(t) and find the time when the cat strikes
the mirror. (Recall that the mirror is a perpendicular bisector of
the line joining an object with its apparent position as seen by
reflection.)
Peter Linnell
2011-06-27