7th Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to noon November 2, 1985
Fill out the individual registration form
- Prove that
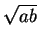 < (a + b)/2 where a and b are positive
real numbers.
< (a + b)/2 where a and b are positive
real numbers.
- Find the remainder r,
1 < r < 13, when 21985 is divided
by 13.
- Find real numbers c1 and c2 so that
where
and I is the identity matrix.
- Consider an infinite sequence
{ck}k = 0
 of circles.
The largest, C0, is centered at (1, 1) and is tangent to both the
x and y-axes. Each smaller circle Cn is centered on the line
through (1, 1) and (2, 0) and is tangent to the next larger circle
Cn - 1 and to the x-axis. Denote the diameter of Cn by dn
for
n = 0, 1, 2,.... Find
of circles.
The largest, C0, is centered at (1, 1) and is tangent to both the
x and y-axes. Each smaller circle Cn is centered on the line
through (1, 1) and (2, 0) and is tangent to the next larger circle
Cn - 1 and to the x-axis. Denote the diameter of Cn by dn
for
n = 0, 1, 2,.... Find
- (a)
- d1
- (b)
-
Sn = 0
 dn
dn
- Find the function f = f (x), defined and continuous on
R+ = {x | 0 < x <
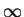 }, that satisfies
f (x + 1) = f (x) + x on
R+ and f (1) = 0.
}, that satisfies
f (x + 1) = f (x) + x on
R+ and f (1) = 0.
- Find an expression for 3/5 as a finite sum of distinct reciprocals of
positive integers. (For example:
2/7 = 1/7 + 1/8 + 1/56.)
- Prove that any positive rational number can be so expressed.
- Let f = f (x) be a real function of a real variable which has
continuous third derivative and which satisfies, for a given c and
all real x,
x =/= c,
(f (x) - f (c))/(x - c) = (f'(x) + f'(c))/2.
Show that
f''(x) = f'(x - f'(c))/(x - c).
- Let
p(x) = a0 + a1x + ... + anxn, where the coefficients
ai are real. Prove that p(x) = 0 has at least one root in the
interval
0 < x < 1 if
a0 + a1/2 + ... + an/(n + 1) = 0.
Peter Linnell
2001-10-03
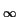 dn
dn