5th Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to 12:00 noon, November 5, 1983
Fill out the individual registration form
- In the expansion of (a + b)n, where n is a natural number, there
are n + 1 dissimilar terms. Find the number of dissimilar terms in
the expansion of (a + b + c)n.
- A positive integer N (in base 10) is called special if the
operation C of replacing each digit d of N by its
nine's-complement 9 - d, followed by the operation R of reversing
the order of the digits, results in the original number. (For
example, 3456 is a special number because
R[(C3456)] = 3456.) Find
the sum of all special positive integers less than one million which
do not end in zero or nine.
- Let a triangle have vertices at O(0, 0), A(a, 0), and B(b, c) in
the (x, y)-plane.
- (a)
- Find the coordinates of a point P(x, y) in the exterior of
DOAB satisfying
area(OAP) = area(OBP) = area(ABP).
- (b)
- Find a point Q(x, y) in the interior of
DOAQ
satisfying
area(OAQ) = area(OBQ) = area(ABQ).
- A finite set of roads connect n towns
T1, T2,..., Tn where
n
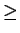 2. We say that towns Ti and Tj (i
2. We say that towns Ti and Tj (i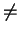 j) are
directly connected if there is a road segment connecting Ti
and Tj which does not pass through any other town. Let f (Tk)
be the number of other towns directly connected to Tk. Prove that
f is not one-to-one.
j) are
directly connected if there is a road segment connecting Ti
and Tj which does not pass through any other town. Let f (Tk)
be the number of other towns directly connected to Tk. Prove that
f is not one-to-one.
- Find the function f (x) such that for all L
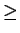 0, the area under
the graph of y = f (x) and above the x-axis from x = 0 to x = L
equals the arc length of the graph from x = 0 to x = L. (Hint:
recall that
d /dx cosh-1x = 1/
0, the area under
the graph of y = f (x) and above the x-axis from x = 0 to x = L
equals the arc length of the graph from x = 0 to x = L. (Hint:
recall that
d /dx cosh-1x = 1/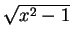 .)
.)
- Let
f (x) = 1/x and
g(x) = 1 - x for
x
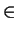 (0, 1). List all
distinct functions that can be written in the form
fogofogo...ofogof where o represents
composition. Write each function in the form
(ax + b)/(cx + d ), and prove that your list is exhaustive.
(0, 1). List all
distinct functions that can be written in the form
fogofogo...ofogof where o represents
composition. Write each function in the form
(ax + b)/(cx + d ), and prove that your list is exhaustive.
- If a and b are real, prove that
x4 + ax + b = 0 cannot have
only real roots.
- A sequence fn is generated by the recurrence formula
fn + 1 = (fnfn - 1 + 1)/fn - 2,
for
n = 2, 3, 4,..., with
f0 = f1 = f2 = 1. Prove that fn
is integer-valued for all integers n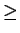 0.
0.
Peter Linnell
2001-08-12