4th Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to 12:00 noon, November 6, 1982
Fill out the individual registration form
- What is the remainder when
X1982 + 1 is divided by X - 1?
Verify your answer.
- A box contains marbles, each of which is red, white or blue. The
number of blue marbles is a least half the number of white marbles
and at most on-third the number of red marbles. The number which
are white or blue is at least 55. Find the minimum possible number
of red marbles.
- Let
a,
b, and
c be vectors such
that
{a,b,c} is linearly
dependent. Show that
| | | |
| |
a·a |
a·b |
a·c |
| |
b·a |
b·b |
b·c |
| |
c·a |
c·b |
c·c |
|
| |
= 0. |
- Prove that
tn - 1 + t1 - n < tn + t-n when t
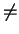 1, t > 0
and n is a positive integer.
1, t > 0
and n is a positive integer.
- When asked to state the Maclaurin Series, a student writes
(incorrectly)
(*) f (x) = f (x) + xf'(x) + x2f''(x)/2! + x3f'''(x)/3! + ....
- (a)
- State Maclaurin's Series for f (x) correctly.
- (b)
- Replace the left-hand side of (*) by a simple closed form expression
in f in such a way that the statement becomes valid (in general).
- Let S be a set of positive integers and let E be the operation on
the set of subsets of S defined by
EA = {x
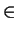 A | x is
even}, where
A
A | x is
even}, where
A 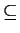 S. Let
CA denote the
complement of A in S.
ECEA will denote
E(C(EA)) etc.
S. Let
CA denote the
complement of A in S.
ECEA will denote
E(C(EA)) etc.
- (a)
- Show that
ECECEA = EA.
- (b)
- Find the maximum number of distinct subsets of S that can be
generated by applying the operations E and
C to a
subset A of S an arbitrary number of times in any order.
- Let p(x) be a polynomial of the form
p(x) = ax2 + bx + c, where
a, b and c are integers, with the property that
1 < p(1) < p(p(1)) < p(p(p(1))). Show that a
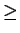 0.
0.
- For n
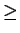 2, define Sn by
Sn = Sk = n
2, define Sn by
Sn = Sk = n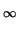 k-2.
k-2.
- (a)
- Prove or disprove that
1/n < Sn < 1/(n - 1).
- (b)
- Prove or disprove that
Sn < 1/(n - 3/4).
Peter Linnell
2001-08-17