2nd Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to 12:00 noon, November 8, 1980
Fill out the individual registration form
- Let * denote a binary operation on a set S with the property that
(
w*
x)*(
y*
z) =
w*
z for all
w,
x,
y,
z 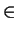 S
S.
- (a)
- If a*b = c, then c*c = c.
- (b)
- If a*b = c, then a*x = c*x for all x
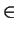 S.
S.
- The sum of the first n terms of the sequence
1, (1 + 2), (1 + 2 + 22),...,(1 + 2 + ... + 2k - 1),...
is of the form
2n + R + Sn2 + Tn + U for all n > 0. Find
R, S, T and U.
- Let
an = (1·3·5·...·(2n - 1))/(2·4·6·...·2n).
- (a)
- Prove that
limn - >
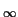 an exists.
an exists.
- (b)
- Show that
an = ((1 - (1/2)2)(1 - (1/4)2)...(1 - (1/2n)2))/((2n + 1)an).
- (c)
- Find
limn - >
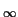 an and justify your answer.
an and justify your answer.
- Let P(x) be any polynomial of degree at most 3. It can be shown
that there are numbers x1 and x2 such that
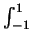 P(x) dx = P(x1) + P(x2), where x1 and x2 are independent
of the polynomial P.
P(x) dx = P(x1) + P(x2), where x1 and x2 are independent
of the polynomial P.
- (a)
- Show that
x1 = - x2.
- (b)
- Find x1 and x2.
- For x > 0, show that
ex < (1 + x)1 + x.
- Given the linear fractional transformation of x into
f1(x) = (2x - 1)/(x + 1), define
fn + 1(x) = f1(fn(x)) for
n = 1, 2, 3,.... It can be shown that
f35 = f5. Determine
A, B, C, and D so that
f28(x) = (Ax + B)/(Cx + D).
- Let S be the set of all ordered pairs of integers (m, n)
satisfying m > 0 and n < 0. Let < be a partial ordering on
S defined by the statement:
(m, n) < (m', n') if and only if m
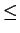 m' and n
m' and n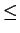 n'. An
example is
(5, - 10) < (8, - 2). Now let O be a completely ordered
subset of S, i.e. if
(a, b)
n'. An
example is
(5, - 10) < (8, - 2). Now let O be a completely ordered
subset of S, i.e. if
(a, b) 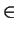 O and
(c, d )
O and
(c, d ) 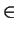 O, then
(a, b) < (c, d ) or
(c, d ) < (a, b). Also let
O denote the
collection of all such completely ordered sets.
O, then
(a, b) < (c, d ) or
(c, d ) < (a, b). Also let
O denote the
collection of all such completely ordered sets.
- (a)
- Determine whether an arbitrary
O
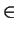 O is finite.
O is finite.
- (b)
- Determine whether the cardinality || O|| of O is bounded for
O
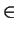 O.
O.
- (c)
- Determine whether || O|| can be countably infinite for any
O
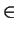 O.
O.
- Let z = x + iy be a complex number with x And y rational and with
| z| = 1.
- (a)
- Find two such complex numbers.
- (b)
- Show that
| z2n - 1| = 2| sinnq|, where
z = eiq.
- (c)
- Show that
| z2n - 1| is rational for every n.
Peter Linnell
2001-08-17
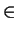 S.
S.
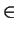 S.
S.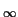 an exists.
an exists.
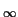 an and justify your answer.
an and justify your answer.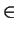 O is finite.
O is finite.
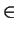 O.
O.
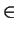 O.
O.