1st Annual
Virginia Tech Regional Mathematics Contest
From 9:30a.m. to 12:00 noon, November 10, 1979
Fill out the individual registration form
- Show that the right circular cylinder of volume V which has the
least surface area is the one whose diameter is equal to its
altitude. (The top and bottom are part of the surface.)
- Let S be a set which is closed under the binary operation o,
with the following properties:
- (i)
- there is an element e
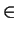 S such that
aoe = eoa = a,
for each a
S such that
aoe = eoa = a,
for each a 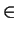 S,
S,
- (ii)
-
(aob)o(cod )= (aoc)o(bod ), for
all
a, b, c, d
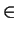 S.
S.
Prove or disprove:
- (a)
- o is associative on S
- (b)
- o is commutative on S
- Let A be an n X n nonsingular matrix with complex elements,
and let
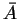 be its complex conjugate. Let
B = A
be its complex conjugate. Let
B = A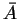 + I, where I is the n X n identity matrix.
+ I, where I is the n X n identity matrix.
- (a)
- Prove or disprove:
A-1BA =
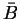 .
.
- (b)
- Prove or disprove: the determinant of
A
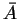 + I is real.
+ I is real.
- Let f (x) be continuously differentiable on
(0,
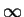 ) and suppose
limx - >
) and suppose
limx - > 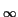 f'(x) = 0. Prove that
limx - >
f'(x) = 0. Prove that
limx - > 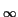 f (x)/x = 0.
f (x)/x = 0.
- Show, for all positive integers
n = 1, 2,..., that 14 divides
34n + 2 + 52n + 1.
- Suppose an > 0 and
Sn = 1
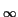 an diverges. Determine
whether
Sn = 1
an diverges. Determine
whether
Sn = 1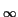 an/Sn2 converges, where
Sn = a1 + a2 + ... + an.
an/Sn2 converges, where
Sn = a1 + a2 + ... + an.
- Let S be a finite set of non-negative integers such that
| x - y|
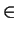 S whenever x, y
S whenever x, y 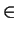 S.
S.
- (a)
- Give an example of such a set which contains ten elements.
- (b)
- If A is a subset of S containing more than two-thirds of the
elements of S, prove or disprove that every element of S
is the sum or difference of two elements from A.
- Let S be a finite set of polynomials in two variables, x and y.
For n a positive integer, define
Wn(S) to be the
collection of all expressions
p1p2...pk, where pi
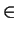 S
and
1
S
and
1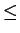 k
k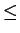 n. Let dn(S) indicate the maximum number of
linearly independent polynomials in
Wn(S). For example,
W2({x2, y}) = {x2, y, x2y, x4, y2} and
d2({x2, y}) = 5.
n. Let dn(S) indicate the maximum number of
linearly independent polynomials in
Wn(S). For example,
W2({x2, y}) = {x2, y, x2y, x4, y2} and
d2({x2, y}) = 5.
- (a)
- Find
d2({1, x, x + 1, y}).
- (b)
- Find a closed formula in n for
dn({1, x, y}).
- (c)
- Calculate the least upper bound over all such sets of
limsupn - >
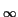 (logdn(S))/log n.
(
limsupn - >
(logdn(S))/log n.
(
limsupn - > 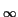 an = limn - >
an = limn - > 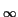 (sup{an, an + 1,...}),
where sup means supremum or least upper bound.)
(sup{an, an + 1,...}),
where sup means supremum or least upper bound.)
Peter Linnell
2001-08-12
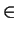 S such that
aoe = eoa = a,
for each a
S such that
aoe = eoa = a,
for each a 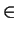 S,
S,
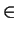 S.
S.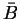 .
.
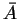 + I is real.
+ I is real.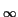 (logdn(S))/log n.
(
limsupn - >
(logdn(S))/log n.
(
limsupn - > 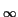 an = limn - >
an = limn - > 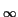 (sup{an, an + 1,...}),
where sup means supremum or least upper bound.)
(sup{an, an + 1,...}),
where sup means supremum or least upper bound.)