37th Annual Virginia Tech Regional Mathematics Contest
From 9:00a.m. to 11:30a.m., October 24, 2015

Fill out the individual registration form

1. Find all integers n for which n⁴ +6n³ +11n² + 3n + 31 is a perfect square.

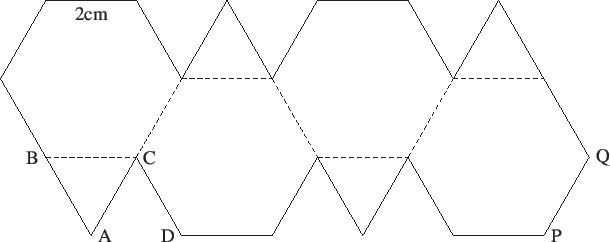
2. The planar diagram below, with equilateral triangles and regular hexagons, sides length 2cm., is folded along the dashed edges of the polygons, to create a closed surface in three dimensional Euclidean spaces. Edges on the periphery of the planar diagram are identified (or glued) with precisely one other edge on the periphery in a natural way. Thus for example, BA will be joined to QP and AC will be joined to DC. Find the volume of the three-dimensional region enclosed by the resulting surface.

   

3. Let (a_i)_1≤i≤2015 be a sequence consisting of 2015 integers, and let (k_i)_1≤i≤2015 be a sequence of 2015 positive integers (positive integer excludes 0). Let

   A =

   (

   	a1k1	a1k2	...	a1k2015
   	a2k1	a2k2	...	a2k2015
   	⋮	⋮	...	⋮
   	a2015k1	a2015k2	...	a2015k2015

   ).

   Prove that 2015! divides det A.

4. Consider the harmonic series ∑_n≥11/n = 1 + 1/2 + 1/3.... Prove that every positive rational number can be obtained as an unordered partial sum of this series. (An unordered partial sum may skip some of the terms 1/k.)

5. Evaluate ∫₀^∞(arctan(πx) - arctan(x))/x dx     (where 0≤arctan(x) < π/2 for 0≤x < ∞).

6. Let (a₁, b₁),...,(a_n, b_n) be n points in ℝ² (where ℝ denotes the real numbers), and let ϵ > 0 be a positive number. Can we find a real-valued function f (x, y) that satisfies the following three conditions?
   1. f (0, 0) = 1;

   2. f (x, y)≠ 0 for only finitely many (x, y)∈ℝ²;

   3. ∑_r=1^r=n| f (x + a_r, y + b_r) - f (x, y)| < ϵ for every (x, y)∈ℝ².
   Justify your answer.

7. Let n be a positive integer and let x₁,..., x_n be n nonzero points in ℝ². Suppose ⟨x_i, x_j⟩ (scalar or dot product) is a rational number for all i, j ( 1≤i, j≤n). Let S denote all points of ℝ² of the form ∑_i=1ⁱ⁼ⁿa_ix_i where the a_i are integers. A closed disk of radius R and center P is the set of points at distance at most R from P (includes the points distance R from P). Prove that there exists a positive number R and closed disks D₁, D₂,... of radius R such that

   (a)

   Each disk contains exactly two points of S;

   (b)

   Every point of S lies in at least one disk;

   (c)

   Two distinct disks intersect in at most one point.