32nd Annual Virginia Tech Regional Mathematics Contest
From 9:00a.m. to 11:30a.m., October 30, 2010

Fill out the individual registration form

1. Let d be a positive integer and let A be a d×d matrix with integer entries. Suppose I + A + A² + ... + A¹⁰⁰ = 0 (where I denotes the identity d×d matrix, so I has 1's on the main diagonal, and 0 denotes the zero matrix, which has all entries 0). Determine the positive integers n≤100 for which Aⁿ + Aⁿ⁺¹ + ... + A¹⁰⁰ has determinant ±1.

2. For n a positive integer, define f₁(n) = n and then for i a positive integer, define f_i+1(n) = f_i(n)^f_i(n). Determine f₁₀₀(75)mod 17 (i.e. determine the remainder after dividing f₁₀₀(75) by 17, an integer between 0 and 16). Justify your answer.

3. Prove that cos(π/7) is a root of the equation 8x³ -4x² - 4x + 1 = 0, and find the other two roots.

4. Let ΔABC be a triangle with sides a, b, c and corresponding angles A, B, C (so a = BC and A = ∠BAC etc.). Suppose that 4A + 3C = 540^o. Prove that (a - b)²(a + b) = bc².

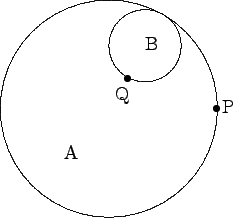
5. Let A, B be two circles in the plane with B inside A. Assume that A has radius 3, B has radius 1, P is a point on A, Q is a point on B, and A and B touch so that P and Q are the same point. Suppose that A is kept fixed and B is rolled once round the inside of A so that Q traces out a curve starting and finishing at P. What is the area enclosed by this curve?

   
   
   

6. Define a sequence by a₁ = 1, a₂ = 1/2, and a_n+2 = a_n+1 - a_na_n+1/2 for n a positive integer. Find lim_{n-> ∞}na_n.

7. Let ∑_n=1^∞a_n be a convergent series of positive terms (so a_i > 0 for all i) and set b_n = 1/(na_n²) for n≥1. Prove that ∑_n=1^∞n/(b₁ + b₂ + ... + b_n) is convergent.