31st Annual Virginia Tech Regional Mathematics Contest
From 9:00a.m. to 11:30a.m., October 24, 2009

Fill out the individual registration form

1. A walker and a jogger travel along the same straight line in the same direction. The walker walks at one meter per second, while the jogger runs at two meters per second. The jogger starts one meter in front of the walker. A dog starts with the walker, and then runs back and forth between the walker and the jogger with constant speed of three meters per second. Let f (n) meters denote the total distance travelled by the dog when it has returned to the walker for the nth time (so f (0) = 0). Find a formula for f (n).

2. Given that 40! =
   abc def 283 247 897 734 345 611 269 596 115 894 272 pqr stu vwx
   find p, q, r, s, t, u, v, w, x, and then find a, b, c, d, e, f.

3. Define f (x) = ∫₀^x∫₀^xe^u2v2 dudv. Calculate 2f''(2) + f'(2) (here f'(x) = df /dx).

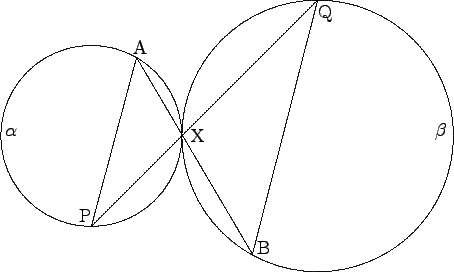
4. Two circles α,β touch externally at the point X. Let A, P be two distinct points on α different from X, and let AX and PX meet β again in the points B and Q respectively. Prove that AP is parallel to QB.

   
   
   

5. Let C denote the complex numbers and let M₃(C) denote the 3 by 3 matrices with entries in C. Suppose A, B∈M₃(C), B≠ 0, and AB = 0 (where 0 denotes the 3 by 3 matrix with all entries zero). Prove that there exists 0≠D∈M₃(C) such that AD = DA = 0.

6. Let n be a nonzero integer. Prove that n⁴ -7n² + 1 can never be a perfect square (i.e. of the form m² for some integer m).

7. Does there exist a twice differentiable function f : R -> R such that f'(x) = f (x + 1) - f (x) for all x and f''(0)≠ 0? Justify your answer. (Here R denotes the real numbers and f' denotes the derivative of f.)