30th Annual Virginia Tech Regional Mathematics Contest
From 9:00a.m. to 11:30a.m., November 1, 2008

Fill out the individual registration form

1. Find the maximum value of xy³ + yz³ + zx³ - x³y - y³z - z³x where 0≤x≤1, 0≤y≤1, 0≤z≤1.

2. How many sequences of 1's and 3's sum to 16? (Examples of such sequences are {1, 3, 3, 3, 3, 3} and {1, 3, 1, 3, 1, 3, 1, 3}.)

3. Find the area of the region of points (x, y) in the xy-plane such that x⁴ + y⁴≤x² - x²y² + y².

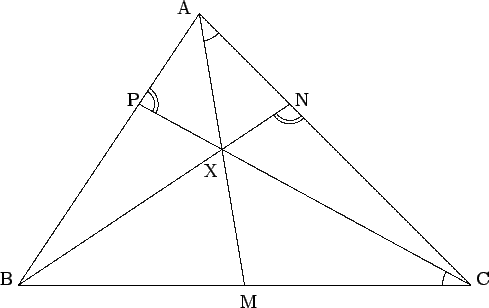
4. Let ABC be a triangle, let M be the midpoint of BC, and let X be a point on AM. Let BX meet AC at N, and let CX meet AB at P. If ∠MAC = ∠BCP, prove that ∠BNC = ∠CPA.

   
   
   

5. Let a₁, a₂,... be a sequence of nonnegative real numbers and let π,ρ be permutations of the positive integers N (thus π,ρ : N --> N are one-to-one and onto maps). Suppose that ∑_n=1^∞a_n = 1 and ε is a real number such that ∑_n=1^∞| a_n - a_πn| + ∑_n=1^∞| a_n - a_ρn| < ε. Prove that there exists a finite subset X of N such that | X∩πX|,| X∩ρX| > (1 - ε)| X| (here | X| indicates the number of elements in X; also the inequalities < , > are strict).

6. Find all pairs of positive (nonzero) integers a, b such that ab - 1 divides a⁴ -3a² + 1.

7. Let f₁(x) = x and f_n+1(x) = x^f_n(x) for n a positive integer. Thus f₂(x) = x^x and f₃(x) = x^(xx). Now define g(x) = lim_{n--> ∞}1/f_n(x) for x > 1. Is g continuous on the open interval (1,∞)? Justify your answer.