29th Annual Virginia Tech Regional Mathematics Contest
From 9:00a.m. to 11:30a.m., October 27, 2007

Fill out the individual registration form

1. Evaluate ∫₀^x(dθ)/(2 + tanθ), where 0≤x≤π/2. Use your result to show that ∫₀^π/4(dθ)/(2 + tanθ) = (π + ln(9/8))/10.

2. Given that e^x = 1/0! + x/1! + x²/2! + ... + xⁿ/n! + ... find, in terms of e, the exact values of

   (a)

   1/1! + 2/3! + 3/5! + ... + n/(2n - 1)! + ... and

   (b)

   1/3! + 2/5! + 3/7! + ... + n/(2n + 1)! + ...

3. Solve the initial value problem dy/dx = y ln y + ye^x, y(0) = 1 (i.e. find y in terms of x).

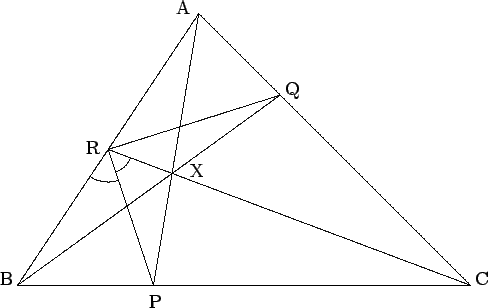
4. In the diagram below, P, Q, R are points on BC, CA, AB respectively such that the lines AP, BQ, CR are concurrent at X. Also PR bisects ∠BRC, i.e. ∠BRP = ∠PRC. Prove that ∠PRQ = 90^o.

   
   
   

   
   

5. Find the third digit after the decimal point of
   (2 + √5)¹⁰⁰((1 + √2)¹⁰⁰ + (1 + √2)^-100).
   For example, the third digit after the decimal point of π = 3.14159... is 1.

6. Let n be a positive integer, let A, B be square symmetric n×n matrices with real entries (so if a_ij are the entries of A, the a_ij are real numbers and a_ij = a_ji). Suppose there are n×n matrices X, Y (with complex entries) such that det(AX + BY)≠ 0. Prove that det(A² + B²)≠ 0 (det indicates the determinant).

7. Determine whether the series ∑_n=2^∞n^{-(1+(ln(ln n))-2)} is convergent or divergent (ln denotes natural log).