28th Annual Virginia Tech Regional Mathematics Contest
From 9:00a.m. to 11:30a.m., October 28, 2006

Fill out the individual registration form

1. Find, and give a proof of your answer, all positive integers n such that neither n nor n² contain a 1 when written in base 3.

2. Let S(n) denote the number of sequences of length n formed by the three letters A,B,C with the restriction that the C's (if any) all occur in a single block immediately following the first B (if any). For example ABCCAA, AAABAA, and ABCCCC are counted in, but ACACCB and CAAAAA are not. Derive a simple formula for S(n) and use it to calculate S(10).

3. Recall that the Fibonacci numbers F(n) are defined by F(0) = 0, F(1) = 1, and F(n) = F(n - 1) + F(n - 2) for n≥2. Determine the last digit of F(2006) (e.g. the last digit of 2006 is 6).

4. We want to find functions p(t), q(t), f (t) such that

   (a)

   p and q are continuous functions on the open interval (0,π).

   (b)

   f is an infinitely differentiable nonzero function on the whole real line (- ∞,∞) such that f (0) = f'(0) = f''(0).

   (c)

   y = sin t and y = f (t) are solutions of the differential equation y'' + p(t)y' + q(t)y = 0 on (0,π).

   Is this possible? Either prove this is not possible, or show this is possible by providing an explicit example of such f, p, q.

5. Let {a_n} be a monotonic decreasing sequence of positive real numbers with limit 0 (so a₁≥a₂≥...≥ 0). Let {b_n} be a rearrangement of the sequence such that for every non-negative integer m, the terms b_3m+1, b_3m+2, b_3m+3 are a rearrangement of the terms a_3m+1, a_3m+2, a_3m+3 (thus, for example, the first 6 terms of the sequence {b_n} could be a₃, a₂, a₁, a₄, a₆, a₅). Prove or give a counterexample to the following statement: the series ∑_n=1^∞(- 1)ⁿb_n is convergent.

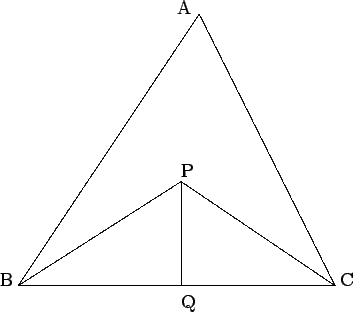
6. In the diagram below BP bisects ∠ABC, CP bisects ∠BCA, and PQ is perpendicular to BC. If BQ.QC = 2PQ², prove that AB + AC = 3BC.

   
   
   

7. Three spheres each of unit radius have centers P, Q, R with the property that the center of each sphere lies on the surface of the other two spheres. Let C denote the cylinder with cross-section PQR (the triangular lamina with vertices P, Q, R) and axis perpendicular to PQR. Let M denote the space which is common to the three spheres and the cylinder C, and suppose the mass density of M at a given point is the distance of the point from PQR. Determine the mass of M.