27th Annual
Virginia Tech Regional Mathematics Contest
From 8:30a.m. to 11:00a.m., October 29, 2005
Fill out the individual registration form
- Find the largest positive integer n with the property that
n + 6(p3 + 1) is prime whenever p is a prime number
such that
2 < p < n. Justify your answer.
- Find, and write out explicitly, a permutation
(p(1), p(2),..., p(20)) of
(1, 2,..., 20) such that k + p(k) is a power of
2 for
k = 1, 2,..., 20, and prove that only one such permutation
exists. (To illustrate, a permutation of
(1, 2, 3, 4, 5) such that
k + p(k) is a power of 2 for
k = 1, 2,..., 5 is clearly
(1, 2, 5, 4, 3), because 1 + 1 = 2, 2 + 2 = 4, 3 + 5 = 8, 4 + 4 = 8, and 5 + 3 = 8.)
- We wish to tile a strip of n 1-inch by 1-inch squares. We can use
dominos which are made up of two tiles which cover two adjacent
squares, or 1-inch square tiles which cover one square. We may cover
each square with one or two tiles and a tile can be above or below a
domino on a square, but no part of a domino can be placed on any part
of a different domino. We do not distinguish whether a
domino is above or below a tile on a given square. Let t(n)
denote the number of ways the strip can be tiled according to the
above rules. Thus for example, t(1) = 2 and t(2) = 8. Find a
recurrence relation for t(n), and use it to compute t(6).
- A cubical box with sides of length 7 has vertices at
(0, 0, 0), (7, 0, 0), (0, 7, 0), (7, 7, 0), (0, 0, 7),
(7, 0, 7), (0, 7, 7), (7, 7, 7). The inside of the box is lined with
mirrors and from the point (0, 1, 2), a beam of light is directed to
the point (1, 3, 4). The light then reflects repeatedly off the
mirrors on the inside of the box. Determine how far the beam of
light travels before it first returns to its starting point at
(0, 1, 2).
- Define
f (x, y) = (xy)/(x2 + (y ln(x2))2) if
x = / = 0, and
f (0, y) = 0 if y = / = 0. Determine whether
lim(x, y)- > (0, 0)f (x, y) exists, and what its value is
if the limit does exist.
- Compute
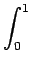 ((e - 1)
((e - 1)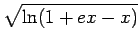 + e(x2)) dx.
+ e(x2)) dx.
- Let A be a
5 X 10 matrix with real entries, and let A'
denote its transpose (so A' is a
10 X 5 matrix, and the
ijth entry of A' is the jith entry of A). Suppose every
5 X 1 matrix with real entries (i.e. column vector in
5 dimensions) can be written in the form
Au where
u is a
10 X 1 matrix with real entries.
Prove that every
5 X 1 matrix with real entries can be written
in the form
AA'v where
v is a
5 X 1
matrix with real entries.
Peter Linnell
2005-10-30