26th Annual
Virginia Tech Regional Mathematics Contest
From 8:30a.m. to 11:00a.m., October 23, 2004
Fill out the individual registration form
- Let I denote the
2 X 2 identity matrix
and let
where A, B, C are arbitrary
2 X 2
matrices which entries in
R, the real numbers. Thus M and N are
4 X 4 matrices
with entries in
R. Is it true that M is invertible
(i.e. there is a
4 X 4 matrix X such that MX = XM = the
identity matrix) implies N is invertible? Justify your answer.
- A sequence of integers {f (n)} for
n = 0, 1, 2,... is defined as
follows: f (0) = 0 and for n > 0,
| f (n) = |
f (n - 1) + 3, if n = 0 or 1 (mod 6), |
|
| |
f (n - 1) + 1, if n = 2 or 5 (mod 6), |
|
| |
f (n - 1) + 2, if n = 3 or 4 (mod 6). |
|
Derive an explicit formula for f (n) when n = 0 (mod 6), showing all
necessary details in your derivation.
- A computer is programmed to randomly generate a string of six symbols
using only the letters A, B, C. What is the probability that the
string will not contain three consecutive A's?
- A
9 X 9 chess board has two squares from opposite corners and
its central square removed (so 3 squares on the same diagonal are
removed, leaving 78 squares). Is it possible to cover the remaining
squares using dominoes, where each domino covers two adjacent
squares? Justify your answer.
- Let
f (x) =
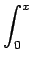 sin(t2 - t + x) dt. Compute
f''(x) + f (x) and deduce that
f(12)(0) + f(10)(0) = 0 (f(10) indicates 10th
derivative).
sin(t2 - t + x) dt. Compute
f''(x) + f (x) and deduce that
f(12)(0) + f(10)(0) = 0 (f(10) indicates 10th
derivative).
(Please turn over)
- An enormous party has an infinite number of people. Each two
people either know or don't know each other. Given a
positive integer n, prove there are n people in the party such
that either they all know each other, or nobody knows each other (so
the first possibility means that if A and B are any two of the n
people, then A knows B, whereas the second possibility means that
if A and B are any two of the n people, then A does not know
B).
- Let {an} be a sequence of positive real numbers such that
limn-->
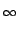 an = 0.
Prove that
Sn=1
an = 0.
Prove that
Sn=1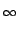 | 1 - an+1/an| is divergent.
| 1 - an+1/an| is divergent.
Peter Linnell
2004-10-29