25th Annual
Virginia Tech Regional Mathematics Contest
From 8:30a.m. to 11:00a.m., November 1, 2003
Fill out the individual registration form
- An investor buys stock worth $10,000 and holds it for n
business days.
Each day he has an equal chance of either gaining 20% or
losing 10%. However
in the case he gains every day (i.e. n gains of 20%), he is
deemed to have lost all his money, because he must have been
involved with insider trading.
Find a (simple) formula, with proof, of the amount of money he will
have on average at the end of the n days.
- Find
Sn = 1
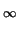 xn/(n(n + 1)) = x/(1*2) + x2/(2*3) + x3/(3*4) + ...
for | x| < 1.
xn/(n(n + 1)) = x/(1*2) + x2/(2*3) + x3/(3*4) + ...
for | x| < 1.
- Determine all invertible 2 by 2 matrices A with complex
numbers as entries satisfying
A = A-1 = A', where A'
denotes the transpose of A.
- It is known that
2cos3p/7 - cos2p/7 - cosp/7 is a rational number.
Write this rational number in the form p/q, where p and q are
integers with q positive.
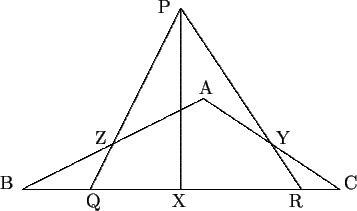
- In the diagram below, X is the midpoint of BC, Y is the
midpoint of
AC, and Z is the midpoint of AB. Also
/ ABC + / PQC = / ACB + / PRB = 90o. Prove that
/ PXC = 90o.
- Let
f : [0, 1] - > [0, 1] be a continuous function such
that
f (f (f (x))) = x for all
x e [0, 1]. Prove that f (x) = x
for all
x e [0, 1]. Here [0, 1] denotes the closed interval
of all real numbers between 0 and 1, including 0 and 1.
- Let T be a solid tetrahedron whose edges all have length 1.
Determine the volume of
the region consisting of points which are at distance at most
1 from some point in T (your answer
should involve
 ,
,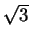 ,p).
,p).
Peter Linnell
2003-11-13

