23rd Annual
Virginia Tech Regional Mathematics Contest
From 8:30a.m. to 11:00a.m., November 3, 2001
Fill out the individual registration form
- Three infinitely long circular cylinders each with unit radius have
their axes along the x, y and z-axes. Determine the volume of
the region common to all three cylinders. (Thus one needs the volume
common to
{y2 + z2 < 1},
{z2 + x2 < 1},
{x2 + y2 < 1}.)
- Two circles with radii 1 and 2 are placed so that they are tangent to
each other and a straight line. A third circle is nestled between
them so that it is tangent to the first two circles and the line.
Find the radius of the third circle.

- For each positive integer n, let Sn denote the total number of
squares in an
n X n square grid. Thus S1 = 1 and S2 = 5, because a
2 X 2 square grid has four
1 X 1 squares
and one
2 X 2 square. Find a recurrence relation for Sn,
and use it to calculate the total number of squares on a chess board
(i.e. determine S8).
- Let an be the nth positive integer k such that the greatest
integer not exceeding
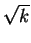 divides k, so the
first few terms of {an} are
{1, 2, 3, 4, 6, 8, 9, 12,...}. Find
a10000 and give reasons to substantiate your answer.
divides k, so the
first few terms of {an} are
{1, 2, 3, 4, 6, 8, 9, 12,...}. Find
a10000 and give reasons to substantiate your answer.
- Determine the interval of convergence of the power series
Sn = 1
 nnxn/n!.
(That is, determine the real numbers x for which the above power
series converges; you must determine correctly whether the series
is convergent at the end points of the interval.)
nnxn/n!.
(That is, determine the real numbers x for which the above power
series converges; you must determine correctly whether the series
is convergent at the end points of the interval.)
- Find a function
f : R+ - > R+ such that
f (f (x)) = (3x + 1)/(x + 3) for all positive real numbers x
(here
R+ denotes the
positive (nonzero) real numbers).
- Let G denote a set of invertible
2 X 2 matrices
(matrices with complex numbers as entries and determinant nonzero)
with the property that if a, b are in G,
then so are ab and a-1.
Suppose there exists a function
f : G - > R with the
property that either
f (ga) > f (a) or
f (g-1a) > f (a)
for all a, g in G with
g =/= I
(here I denotes the identity matrix,
R denotes the real numbers, and the inequality signs are
strict inequality). Prove that given nonempty finite subsets A, B of G,
there is a matrix in G which can be written in exactly one way
in the form xy with x in A and y in B.
Peter Linnell
2001-11-04

