22nd Annual
Virginia Tech Regional Mathematics Contest
From 8:30a.m. to 11:00a.m., October 28, 2000
Fill out the individual registration form
- Evaluate
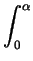 dq/(5 - 4cosq) (your answer will involve inverse
trig functions; you may assume that
0
dq/(5 - 4cosq) (your answer will involve inverse
trig functions; you may assume that
0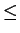 a < p).
Use your answer to show that
a < p).
Use your answer to show that
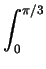 dq/(5 - 4cosq) = 2p/9.
dq/(5 - 4cosq) = 2p/9.
- Let n be a positive integer and let A be an n X n matrix
with real numbers as entries. Suppose
4A4 + I = 0, where I
denotes the identity matrix. Prove that the trace of A (i.e. the
sum of the entries on the main diagonal) is an integer.
- Consider the initial value problem
y' = y2 - t2; y(0) = 0
(where
y' = dy/dt).
Prove that
limt - >
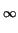 y'(t) exists, and
determine its value.
y'(t) exists, and
determine its value.
-
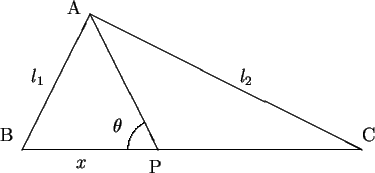
In the above diagram,
l1 = 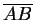 ,
l2 =
,
l2 = 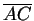 ,
x =
,
x = 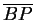 , and
l =
, and
l = 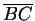 , where
, where
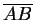 indicates the length of AB. Prove that
l2 - l1 =
indicates the length of AB. Prove that
l2 - l1 = 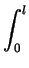 cos(q(x)) dx.
cos(q(x)) dx.
- Two diametrically opposite points P, Q lie on an infinitely
long cylinder which has radius
2/p. A piece of string with
length 8 has its ends joined to P, is wrapped once round
the outside of the cylinder, and then has its midpoint joined to Q
(so there is length 4 of the string on each side of the cylinder).
A paint brush is attached to the
string so that it can slide along the full length
the string. Find the area of the outside surface of the cylinder
which can be painted by the brush.
- Let an (n
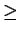 1) be the sequence of numbers defined by the
recurrence relation
1) be the sequence of numbers defined by the
recurrence relation
a1 = 1, an = an - 1a1 + an - 2a2 + ... + a2an - 2 + a1an - 1
(so
a2 = a12 = 1,
a3 = 2a1a2 = 2 etc.).
Prove that
Sn = 1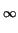 (2/9)nan = 1/3.
(2/9)nan = 1/3.
- Two types of domino-like rectangular tiles,
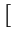
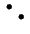
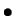
![$ \left.\vphantom{\begin{smallmatrix}
\bullet&\\
&\bullet
\end{smallmatrix}\bigm\vert
\scriptstyle{\ \bullet\ }
}\right]$](img16.gif) and
and
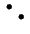
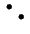
![$ \left.\vphantom{\begin{smallmatrix}
\bullet&\\
&\bullet
\end{smallmatrix}\bigm\vert
\begin{smallmatrix}
\bullet&\\
&\bullet
\end{smallmatrix}}\right]$](img18.gif) ,
are available. The first type may be rotated end-to-end to produce
a tile of type
,
are available. The first type may be rotated end-to-end to produce
a tile of type
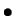
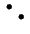
![$ \left.\vphantom{
\scriptstyle{\ \bullet\ }
\bigm\vert
\begin{smallmatrix}
\bullet&\\
&\bullet
\end{smallmatrix}}\right]$](img20.gif) .
Let A(n) be the number of distinct chains of n tiles, placed
end-to-end, that may be constructed if abutting ends are required to
have the same number of dots.
.
Let A(n) be the number of distinct chains of n tiles, placed
end-to-end, that may be constructed if abutting ends are required to
have the same number of dots.
Example A(2) = 5, since the following five chains of
length two, and no others, are allowed.
- (a)
- Find A(3) and A(4).
- (b)
- Find, with proof, a three-term recurrence formula for A(n + 2) in
terms of A(n + 1) and A(n), for
n = 1, 2,..., and use it to find
A(10).
Peter Linnell
2000-10-30

![]() ,
l2 =
,
l2 = ![]() ,
x =
,
x = ![]() , and
l =
, and
l = ![]() , where
, where
![]() indicates the length of AB. Prove that
l2 - l1 =
indicates the length of AB. Prove that
l2 - l1 = ![]() cos(q(x)) dx.
cos(q(x)) dx.
![\begin{multline*}
\left[
\scriptstyle{\ \bullet\ }
\bigm\vert
\begin{smallmatrix...
...egin{smallmatrix}
\bullet&\\
&\bullet
\end{smallmatrix}\right].
\end{multline*}](img21.gif)