- (a)
- Let x
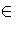 R/rad I and suppose xn = 0 where n > 0. Then
we may write x = y +radl I where y
R/rad I and suppose xn = 0 where n > 0. Then
we may write x = y +radl I where y 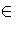 R. Since xn = 0, we
see that yn +rad I =rad I, which means that yn
R. Since xn = 0, we
see that yn +rad I =rad I, which means that yn 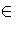 rad I.
By definition of rad I we see that
(yn)m = 0. Therefore
ymn = 0, hence y
rad I.
By definition of rad I we see that
(yn)m = 0. Therefore
ymn = 0, hence y 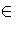 rad I and we deduce that x = 0. This establishes that R/rad I has no nonzero nilpotent
elements.
rad I and we deduce that x = 0. This establishes that R/rad I has no nonzero nilpotent
elements.
- (b)
- If
x
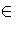 P1
P1 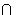 P2
P2 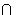 ...
... 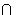 Pn, then x
Pn, then x 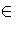 Pi
for all i and hence
xn
Pi
for all i and hence
xn 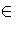 P1P2... Pn. It follows that
x
P1P2... Pn. It follows that
x 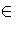 rad
(P1P2... Pn). Conversely suppose x
rad
(P1P2... Pn). Conversely suppose x 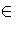 rad
(P1P2... Pn). Then x
rad
(P1P2... Pn). Then x 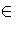 rad Pi for all i. This
means that
xm
rad Pi for all i. This
means that
xm 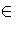 Pi for some m > 0 and since Pi is prime, we
deduce that x
Pi for some m > 0 and since Pi is prime, we
deduce that x 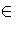 Pi for all i as required.
Pi for all i as required.
- (c)
- If Pi is contained in every Pj, then
P1
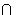 ...
... 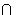 Pn = Pi and hence R/rad
(P1... Pn) = R/Pi by (b). We deduce that R/rad
(P1... Pn) is an integral
domain.
Pn = Pi and hence R/rad
(P1... Pn) = R/Pi by (b). We deduce that R/rad
(P1... Pn) is an integral
domain.
Conversely suppose R/rad (P1... Pn) is an integral domain. Then by (b) we see that R/(P1
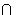 ...
... 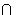 Pn)
is also an integral
domain. Suppose there does not exist an i such that Pi is
contained in Pj for all j. Then for each i, we can choose
xi
Pn)
is also an integral
domain. Suppose there does not exist an i such that Pi is
contained in Pj for all j. Then for each i, we can choose
xi 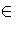 Pi such that
xi
Pi such that
xi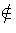 Pj for some j (where j depends on
i). Now set
yi = xi + P1
Pj for some j (where j depends on
i). Now set
yi = xi + P1 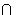 ...
... 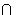 Pn
for
i = 1,..., n.
Then yi is a nonzero element of
R/(P1
Pn
for
i = 1,..., n.
Then yi is a nonzero element of
R/(P1 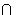 ...
...  Pn)
for all i, yet
Pn)
for all i, yet
y1... yn = x1... xn + P1
This shows that R/(P1 ...
...  Pn = 0
Pn = 0
 ...
... 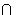 Pn) is not an integral
domain and we have a contradiction. This completes the proof.
Pn) is not an integral
domain and we have a contradiction. This completes the proof.
8 = [K(![]() ) : K] = [K(
) : K] = [K(![]() ) : K(
) : K(![]() )][K(
)][K(![]() ) : K]
) : K]
- (a)
- Let T denote the ideals of R which have trivial
intersection with S. Since a is not nilpotent, we see that
0
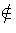 S and hence 0
S and hence 0 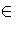 T. Therefore T is
nonempty. Moreover T is ordered by inclusion, and the
union of a chain in T is still in T. It now
follows from Zorn's lemma that T has maximal elements;
let P be one of these maximal elements. Then
P
T. Therefore T is
nonempty. Moreover T is ordered by inclusion, and the
union of a chain in T is still in T. It now
follows from Zorn's lemma that T has maximal elements;
let P be one of these maximal elements. Then
P 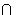 S =
S = 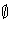 . We claim that P is prime. If P is not a prime ideal,
then there exist ideals A, B strictly containing P such that
AB
. We claim that P is prime. If P is not a prime ideal,
then there exist ideals A, B strictly containing P such that
AB 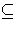 P. By maximality of P we have ai
P. By maximality of P we have ai 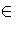 A and aj
A and aj 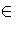 B for some i, j and hence
ai + j
B for some i, j and hence
ai + j 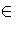 P. This contradicts the
fact that P
P. This contradicts the
fact that P 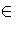 T, and it follows that P is a prime
ideal not containing a.
T, and it follows that P is a prime
ideal not containing a.
- (b)
- Let
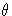 : R
: R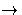 K denote the
composition of the natural epimorphism R
K denote the
composition of the natural epimorphism R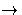 R/P followed by the natural monomorphism R/P
R/P followed by the natural monomorphism R/P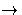 K. If b
K. If b 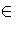 S, then
b
S, then
b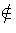 P, hence the image of b in R/P is nonzero and
we deduce that
P, hence the image of b in R/P is nonzero and
we deduce that 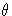 b is invertible in K. It follows that
b is invertible in K. It follows that
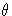 extends to a ring homomorphism
extends to a ring homomorphism
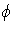 : S-1R
: S-1R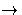 K.
K.
- (a)
- The proper subfields of F containing K are in a one-one correspondence with the proper subgroups of Gal(F/K). Therefore we need to show that S4 has at least 9 proper subgroups. There are 6 elements of order 2 and 8 elements of order 3 in S4. Since any two subgroups of order 2 or 3 intersect in the identity, we see that there are 6 subgroups of order 2 and 4 subgroups of order 3, and we have shown that Gal(F/K) has at least 10 proper subgroups. This finishes part (a).
- (b)
- The Galois extensions E of K in F correspond to the normal
subgroups of Gal(F/K), so we need a nontrivial normal
subgroup of Gal(F/K). The simplest one is the alternating subgroup
A4 of S4. The corresponding subfield E of K is the elements
of F fixed by A4. Also Gal
(E/K)
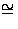 S4/A4
S4/A4 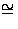
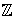 /2
/2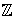 .
.
|
|
|
|