Qualifying Exam Algebra Spring 1995

1. Determine, up to isomorphism, all groups of order .
2. Let G be a noncyclic nilpotent group. Show that there is a normal subgroup N of G such that G/N is a noncyclic abelian group.
3. Describe all finitely generated abelian groups G such that if A and B are subgroups of G, then either or .
4. Let R be a commutative ring with a 1. Recall that if I is an ideal, then is also an ideal. Let P₁, ... ,P_n be distinct prime ideals in R.
   1. Show that 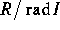has no nonzero nilpotent elements.
   2. Prove that .
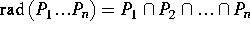   3. Prove that 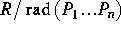is an integral domain if and only if there exists an i such that P_i is contained in every P_j for j=1, ... , n.

5. Suppose that K is a subfield of a field L. Assume that , where . Note that . Let such that . Prove that .
6. Let R be a commutative ring with 1 and let be non-nilpotent. Let .
   1. Prove that there is a prime ideal P not containing a.
   2. Let K be the quotient field of R/P. Prove that there exists a ring homomorphism .

7. Let F be a finite Galois extension of K and suppose that .
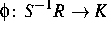   1. Show that there are at least 9 different proper intermediate fields between F and K.
   2. Show that there is a proper Galois extension E of K (in F) and describe the Galois group of E over K.
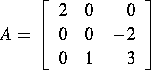8. Find the Jordan canonical form of viewed as matrices over the complex numbers . Find all -matrices with entries in that commute with this canonical form.

Return to

• Algebra Prelims Index
• Peter Linnell's Homepage

 
• About this document ...