We prove that G is not isomorphic to S3 by showing it has an
element whose order is a multiple of 4 or ![]() , which will
establish the result because the orders of elements in S3 are 1,2
and 3. We shall use bars to denote the image of a number in
, which will
establish the result because the orders of elements in S3 are 1,2
and 3. We shall use bars to denote the image of a number in
![]() /4
/4![]() . Thus
. Thus ![]() is the identity of
is the identity of
![]() /4
/4![]() under the operation of addition.
Define
h : F
under the operation of addition.
Define
h : F![]()
![]() /4
/4![]() by
h(x) =
by
h(x) = ![]() and
h(y) =
and
h(y) = ![]() .
Since
h(x6) = 6*
.
Since
h(x6) = 6*![]() =
= ![]() ,
h(y4) = 4*
,
h(y4) = 4*![]() , and
, and
h(yxy-1) = ![]() +
+ ![]() -
- ![]() =
= ![]() = h(x-1),
= h(x-1),
- (i)
- Since R is not a field, we may choose
0
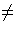 s
s 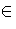 R such
that s is not a unit, equivalently sR
R such
that s is not a unit, equivalently sR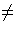 R. Define
f : R
R. Define
f : R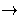 R by f (r) = sr. Then f is an R-module homomorphism which
is injective, because R is a PID and s
R by f (r) = sr. Then f is an R-module homomorphism which
is injective, because R is a PID and s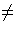 0, and is not onto because
s is not a unit. This proves that R is isomorphic to the proper
submodule sR of R.
0, and is not onto because
s is not a unit. This proves that R is isomorphic to the proper
submodule sR of R.
- (ii)
- Using the fundamental structure theorem for finitely generated
modules over a PID, we may write M as a direct sum of cyclic
R-modules. Since M is not a torsion module, at least one of these
summands must be R; in other words we may write
M
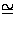 R
R 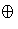 N
for some R-submodule N of M. Then
M
N
for some R-submodule N of M. Then
M 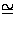 sR
sR 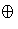 N and since
sR
N and since
sR 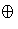 N is a proper submodule of
R
N is a proper submodule of
R 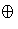 N, we have proven
that M is isomorphic to a proper submodule of itself.
N, we have proven
that M is isomorphic to a proper submodule of itself.
- (i)
- We will write mappings on the left.
Let
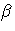 : B
: B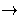 B
B 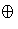 C,
C,
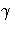 : C
: C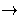 B
B 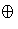 C
denote the natural injections (so
C
denote the natural injections (so
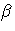 b = (b, 0)), and let
b = (b, 0)), and let
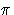 : B
: B 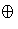 C
C B,
B,
 : B
: B  C
C C
denote the natural epimorphisms (so
C
denote the natural epimorphisms (so
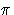 (b, c) = b). Define
(b, c) = b). Define
by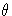 : HomR(A, B
: HomR(A, B 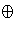 C)
C)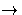 HomR(A, B)
HomR(A, B) 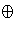 HomR(A, C)
HomR(A, C)
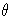 (f )= (
(f )= (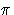 f,
f,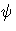 f ), and
f ), and
by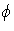 : HomR(A, B)
: HomR(A, B) 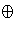 HomR(A, C)
HomR(A, C)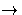 HomR(A, B
HomR(A, B 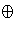 C)
C)
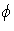 (f, g) =
(f, g) = 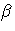 f +
f + 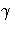 g.
It is easily checked that
g.
It is easily checked that 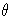 and
and 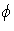 are R-module
homomorphisms, so
will suffice to prove that
are R-module
homomorphisms, so
will suffice to prove that
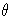
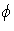 and
and
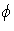
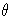 are the
identity maps. We have
are the
identity maps. We have
because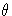
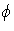 (f, g) =
(f, g) = 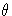 (
(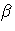 f +
f + 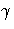 g) = (
g) = (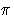 (
(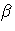 f +
f + 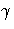 g),
g),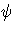 (
(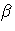 f +
f + 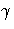 g)) = (f, g)
g)) = (f, g)
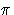
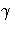 ,
,
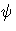
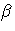 are the zero maps, and
are the zero maps, and 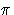
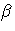 ,
,
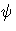
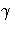 are the identity maps. Therefore
are the identity maps. Therefore
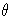
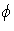 is the identity map. Also
is the identity map. Also
because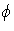
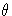 (h) =
(h) = 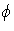 (
(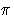 h,
h,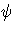 h) =
h) = 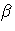
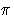 h +
h + 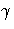
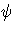 h = (
h = (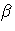
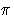 +
+ 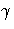
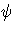 )h = h
)h = h
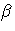
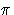 +
+ 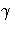
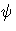 is the identity map. Thus
is the identity map. Thus
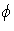
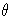 is the identity map and (i) is proven.
is the identity map and (i) is proven.
- (ii)
- Write
HomR(A, A) = X. If
HomR(A, A
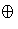 A)
A) 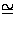
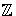 , then by the first part we would have
X
, then by the first part we would have
X 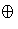 X
X 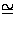
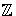 . Thus X
. Thus X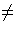 0, and we see that
0, and we see that
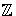 is the direct sum of
two nonzero groups. This is not possible and the result follows.
is the direct sum of
two nonzero groups. This is not possible and the result follows.
- (i)
- Let I be an ideal of S-1R. We need to prove that I is
finitely generated. Let
J = {r
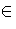 R | r/1
R | r/1 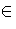 S-1I}
(where we view S-1R as elements of the form r/s where r
S-1I}
(where we view S-1R as elements of the form r/s where r 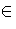 R
and s
R
and s 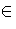 S). Then J is an ideal of R and since R is
Noetherian, there exist elements
x1,..., xn which generate
J as an ideal, which means
J = x1R + ... + xnR. We claim that
I is generated by
{x1/1,..., xn/1} . Indeed if r/s
S). Then J is an ideal of R and since R is
Noetherian, there exist elements
x1,..., xn which generate
J as an ideal, which means
J = x1R + ... + xnR. We claim that
I is generated by
{x1/1,..., xn/1} . Indeed if r/s 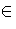 I, then
r = r1x1 + ... + rnxn for some ri
I, then
r = r1x1 + ... + rnxn for some ri 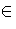 R, and
hence
r/s = r1/s x1 + ... + rn/s xn. This proves
(i).
R, and
hence
r/s = r1/s x1 + ... + rn/s xn. This proves
(i).
- (ii)
- Let S be the multiplicative subset
{1, X, X2,...} .
Then every element of S is invertible in
R[[X, X-1]] and hence
the identity map
R[[X]]
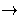 R[[X]] extends to a homomorphism
S-1R[[X]]
R[[X]] extends to a homomorphism
S-1R[[X]]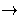 R[[X, X-1]]. It is easily checked that this
map is an isomorphism. Since R[[X]] is Noetherian, it follows
from (i) that
S-1R[[X]] is Noetherian and hence
R[[X, X-1]]
is Noetherian as required.
R[[X, X-1]]. It is easily checked that this
map is an isomorphism. Since R[[X]] is Noetherian, it follows
from (i) that
S-1R[[X]] is Noetherian and hence
R[[X, X-1]]
is Noetherian as required.
- (i)
- Set Y = X - 1. Then
Applying Eisenstein's criterion for the prime 5, we see that Y4 + 5Y3 + 10Y2 + 10Y + 5 is irreducible inX4 + X3 + X2 + X + 1 = (X5 - 1)/(X - 1) = ((Y + 1)5 - 1)/Y = (Y5 + 5Y4 + 10Y3 + 10Y2 + 5Y)/Y = Y4 + 5Y3 + 10Y2 + 10Y + 5. 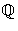 [Y]. Since
Y
[Y]. Since
Y 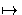 Y + 1 induces an automorphism of
Y + 1 induces an automorphism of
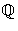 [Y], we
deduce that
X4 + X3 + X2 + X + 1 is irreducible.
[Y], we
deduce that
X4 + X3 + X2 + X + 1 is irreducible.
- (ii)
- Let c(X) denote the characteristic polynomial of A, and let m(X) denote the minimum polynomial of A. Since A5 = I, we see that m(X) divides X5 - 1, and since 1 is not an eigenvalue of A, we see that X - 1 does not divide m(X). Therefore m(X) divides X4 + X3 + X2 + X + 1 and using (i), we deduce that the only irreducible factor of m(X) is X4 + X3 + X2 + X + 1. It follows that the only irreducible factor of c(X) is X4 + X3 + X2 + X + 1, which shows that the degree of c(X) is a multiple of 4. This completes the proof, because n is the degree of c(X).