- Since the action is transitive, all the stabilizers are
conjugate and we see that the stabilizer of any element of X has no
element of finite order other than 1. Thus if f
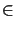 G has finite
order larger than 1, then f cannot be in the stabilizer of any
element of X, and it follows that f cannot fix any element of X.
G has finite
order larger than 1, then f cannot be in the stabilizer of any
element of X, and it follows that f cannot fix any element of X.
- Suppose now that f has prime order q. Then the orbits of < f > have order dividing q. Since q is prime, these orbits have order 1 or q. But if one of the orbits has order 1, then f fixes the element in that orbit which contradicts the above. Therefore all orbits of < f > have order q, and it follows that q divides | X| as required.
Conversely suppose M is a direct summand of a free module F.
First we show that F satisfies the given condition. Let
f : N - > N' be a surjection of R-modules and let
h : F - > N' be
any R-map. Let
{ei | i ![]() I} be an R-basis for F,
where I is some indexing set. Since h is surjective, we may
choose ni
I} be an R-basis for F,
where I is some indexing set. Since h is surjective, we may
choose ni ![]() N such that
f (ni) = h(ei) for all i. Now we
can define g
N such that
f (ni) = h(ei) for all i. Now we
can define g ![]() HomR(F, N) by
g(ei) = ni for all i, and then
fg(ei) = h(ei) for all i. Thus fg = h, and we have proved
the result in the case M = F.
HomR(F, N) by
g(ei) = ni for all i, and then
fg(ei) = h(ei) for all i. Thus fg = h, and we have proved
the result in the case M = F.
For the general case, write
F = M ![]() P as R-modules, and let
y: M - > F be the natural monomorphism
Then we have a commutative diagram
P as R-modules, and let
y: M - > F be the natural monomorphism
Then we have a commutative diagram
| HomR(F, N) | f* - > | HomR(F, N') | |
| y
* |
|
||
| HomR(M, N) | f* - > | HomR(M, N') |