Algebra Preliminary Exam, Spring 1993
Do six problems
- 1.
- Let R be a principal ideal domain. Assume that M is a
nonzero finitely generated R-module with the property that the
intersection of any two nonzero submodules is nonzero. Prove that
M
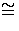 R/Rt where t is either zero or some power of an irreducible
element in R.
R/Rt where t is either zero or some power of an irreducible
element in R.
- 2.
- Let G be a group which acts transitively on a finite set X.
Assume that there is an element x0
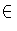 X whose stabilizer has no
element of finite order other than 1.
X whose stabilizer has no
element of finite order other than 1.
- (a)
- Show that if f
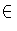 G has finite order larger than 1, then f
has no fixed points.
G has finite order larger than 1, then f
has no fixed points.
- (b)
- Show that if the order of f
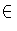 G is a prime q, then
| X|
G is a prime q, then
| X| 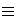 0 mod q.
0 mod q.
- 3.
- Let S be a commutative ring with prime ideals
P1, P2,..., Pt. Show that if
S/P1
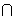 P2
P2 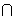 ...
... 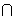 Pt
is a finite set, then each of the Pi is a maximal ideal.
Pt
is a finite set, then each of the Pi is a maximal ideal.
- 4.
- Let p be a prime. Prove that if every
nontrivial finite field extension
of the field F has degree divisible by p, then every finite field
extension of F has degree a power of p. (You may assume that
charF = 0.)
- 5.
- Let R be a commutative ring with a 1. If M and N are
R-modules, then Hom(M, N) denotes the set of all R-module
homomorphisms from M to N. If f : N - > N' is an R-module
homomorphism, then f* : Hom(M, N) - > Hom(M, N') is defined by
f*(g) = fog, the composition of g followed by f. Prove
that M is a projective R-module if and only if for all surjective
f : N - > N', the function f* is surjective.
- 6.
- Let D be a finite dihedral group, and let V be a finite
dimensional complex vector space which is a D-module. (You may
regard D as a group of linear transformations from V to itself.)
Prove that if the only D-invariant subspaces of V are 0 and V
itself (i.e. V is a simple or irreducible D-module), then
dim
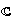 V
V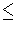 2.
2.
- 7.
- Determine the Galois group of (the splitting field for) the
polynomial
X10 - 1 over the rational numbers.
Peter Linnell
1999-05-31
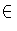 G has finite order larger than 1, then f
has no fixed points.
G has finite order larger than 1, then f
has no fixed points.
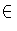 G is a prime q, then
| X|
G is a prime q, then
| X| 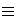 0 mod q.
0 mod q.