Algebra Prelim, Spring 1992
Answer all questions
- 1.
- (a)
- Let G be a finite group of order m , and let p be the
smallest prime which divides m . Prove that if H is a subgroup of
index p , then H is a normal subgroup of G .
- (b)
- Prove that any group of order p 2q is solvable, where p
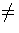 q are primes. (Hint: consider separately the cases p > q and p < q ).
q are primes. (Hint: consider separately the cases p > q and p < q ).
- 2.
- List all groups of order 6 (up to isomorphism), and prove
that they are the only ones.
- 3.
- If A and B are finitely generated abelian groups with A
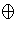 A isomorphic to B
A isomorphic to B 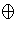 B , prove that A and B are
isomorphic.
B , prove that A and B are
isomorphic.
- 4.
- Suppose
0
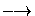 A
A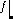
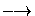 B
B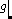
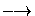 C
C 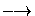 0
is a short exact sequence of modules over a ring R . Prove that if the
sequence splits, i.e. there is an R -module homomorphism h : C
0
is a short exact sequence of modules over a ring R . Prove that if the
sequence splits, i.e. there is an R -module homomorphism h : C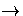 B such that gh = 1C , then
B
B such that gh = 1C , then
B 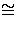 A
A 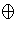 C .
C .
- 5.
- Let R be a commutative ring with a 1. If S is a
multiplicative set (i.e.
x,y
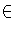 S
S 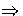 xy
xy 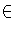 S ) containing
1, but not 0, prove there exists a prime ideal of P of R with
P
S ) containing
1, but not 0, prove there exists a prime ideal of P of R with
P 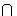 S =
S = 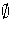 .
.
- 6.
- Let A be an abelian group and let m > 1 be an integer.
Prove that
A
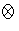
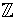 /m
/m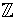
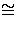 A/mA .
A/mA .
- 7.
- Let K/k be a Galois extension of fields and let
f (x)
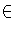 k[x] be an irreducible polynomial which has a root in K . Prove
that f (x) splits into linear factors in K[x] .
k[x] be an irreducible polynomial which has a root in K . Prove
that f (x) splits into linear factors in K[x] .
- 8.
- Let K be a finite Galois extension of
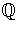 with Galois
group isomorphic to A4 .
For each divisor d of 12, how many subfields
L of K have [K : L] = d ? In each case give the isomorphism class
of
with Galois
group isomorphic to A4 .
For each divisor d of 12, how many subfields
L of K have [K : L] = d ? In each case give the isomorphism class
of 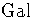 (K/L) , and state whether or not
L/
(K/L) , and state whether or not
L/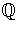 is a Galois
extension. (Recall A4 is a counter-example to the converse of
Lagrange's theorem.)
is a Galois
extension. (Recall A4 is a counter-example to the converse of
Lagrange's theorem.)
Peter Linnell
8/13/1997
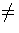 q are primes. (Hint: consider separately the cases p > q and p < q ).
q are primes. (Hint: consider separately the cases p > q and p < q ).