Qualifying Exam Algebra Spring 1991
- 1.
- Suppose that A,H are normal subgroups of a group G such that
G/A is a simple group of order n .
- (a)
- Prove that H
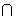 A is a normal subgroup of H .
A is a normal subgroup of H .
- (b)
- Prove that either
H
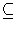 A or H/(H
A or H/(H 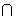 A) is a simple
group of order n . (Hint: use an isomorphim theorem.)
A) is a simple
group of order n . (Hint: use an isomorphim theorem.)
- 2.
- (a)
- Prove that a group of order 100 cannot be simple.
- (b)
- Describe all abelian groups of order 100 up to isomorphism.
- (c)
- Either show that every group of order 100 is abelian, or
exhibit a nonabelian example.
- 3.
- Let G be a group and let f : G
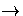 H be a group
homomorphism. Prove that if H is a solvable group and if ker (f )
is abelian, then G is a solvable.
H be a group
homomorphism. Prove that if H is a solvable group and if ker (f )
is abelian, then G is a solvable.
- 4.
- Let R be a PID.
- (a)
- Prove that the intersection of two nonzero maximal ideals cannot
be zero.
- (b)
- Assume that R contains an infinite number of maximal ideals.
Show that the intersection of all the nonzero maximal ideals of R
equals zero.
- 5.
- Let
R
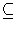 S be rings with a 1 such that S/R is a free
left R -module. Prove that if L is a left ideal of R , then
LS
S be rings with a 1 such that S/R is a free
left R -module. Prove that if L is a left ideal of R , then
LS 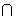 R = L . (Hint: write S as a direct sum of R -modules.)
R = L . (Hint: write S as a direct sum of R -modules.)
- 6.
- Let R be a ring with 1. A nonzero left R -module S is
simple if 0 and S are the only submodules of S . Let
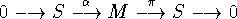
be a short exact sequence of R -modules which is not split,
and such that S is a simple R -module. Show that the only nonzero
submodules of M are 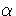 (S) and M . (Hint: if
0
(S) and M . (Hint: if
0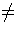 N
N 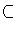 M and
M and
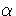 (S)
(S) 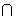 N = 0 , show that there is an isomorphism
N = 0 , show that there is an isomorphism
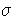 : S
: S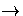 N such that
N such that
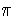
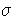 = 1S .)
= 1S .)
- 7.
- Suppose that F is a Galois extension of
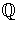 with
[F :
with
[F : 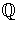 ] = 25 . What possible groups can occur as the Galois
group of F over
] = 25 . What possible groups can occur as the Galois
group of F over 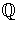 ? In all cases, describe the
intermediate fields between F and
? In all cases, describe the
intermediate fields between F and 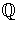 is in terms of inclusion
and dimension over
is in terms of inclusion
and dimension over 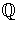 . Which intermediate fields are Galois
over
. Which intermediate fields are Galois
over 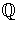 ?
?
- 8.
- Recall that a group G of permutations of a set S is called
transitive if given s,t
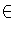 S , then there exists
S , then there exists
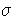
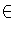 G such that
G such that
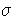 (s) = t . Let f (x) be a separable polynomial in
K[x] and let F be a splitting field of f (x) over K . Prove
that f (x) is irreducible over K if and only if the Galois group of
F over K is a transitive subgroup when viewed as permutations of
the roots of f (x) .
(s) = t . Let f (x) be a separable polynomial in
K[x] and let F be a splitting field of f (x) over K . Prove
that f (x) is irreducible over K if and only if the Galois group of
F over K is a transitive subgroup when viewed as permutations of
the roots of f (x) .
Peter Linnell
8/13/1997
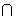 A is a normal subgroup of H .
A is a normal subgroup of H .
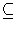 A or H/(H
A or H/(H 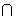 A) is a simple
group of order n . (Hint: use an isomorphim theorem.)
A) is a simple
group of order n . (Hint: use an isomorphim theorem.)