Algebra Preliminary Exam, Spring 1988

Do all eight problems

1. Let G be a group and define by .
   1. Find necessary and sufficient conditions on G such that 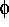is a homomorphism.
   2. Under the conditions determined for (a), prove that 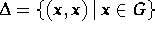is a normal subgroup of G and .
2. Let be a group homomorphism with H an abelian group. Suppose that N is a subgroup of G containing . Prove that N is a normal subgroup of G.
3. Let G be a group of order 99.
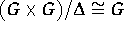   1. Show that G is not a simple group.
   2. Show that G contains a subgroup of order 33.
4. Prove that a finite abelian group is either cyclic or has at least p elements of order p for some prime p.
5. If S is a simple nonabelian group, prove that contains a subgroup isomorphic to S. (Hint: consider conjugation.)
6. Let R be a commutative ring with identity. A simple R-module S is a module whose only submodules are 0 and S.
   1. Prove that an R-module S is simple if and only if there is a maximal ideal such that S is isomorphic to .
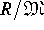   2. Let R be a commutative ring with identity. Show that simple R-modules exist.
7. Let R be a ring with identity and let I be a (two-sided) ideal in R. Let M and N be R-modules.
   1. Show that 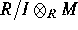is isomorphic to M/IM as left R/I-modules.
   2. Show that 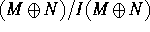is isomorphic to 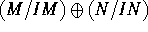. You may use any results about tensor products you know.
8. Let E be an extension field of F with [E:F] = 11. Prove that if with neither in F and if is an F-automorphism of E, then

   

Return to

• Algebra Prelims Index
• Peter Linnell's Homepage

 
• About this document ...