- Let R be a PID and let S be a multiplicatively closed subset. Show that S-1R is a PID.
- Give an example of a PID with exactly 3 nonassociate irreducible elements.
- Find a basis for
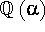 over
over 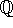 . Justify
y our answer.
. Justify
y our answer.
- Express
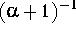 in terms of the basis.
in terms of the basis.
- Express
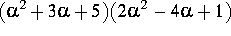 in
terms of the basis.
in
terms of the basis.