Algebra Preliminary Exam, Spring 1984
Do all problems
- 1.
- Find the Galois group of x6 - 1 over
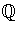 .
.
- 2.
- Show that a semisimple right Artinian
ring without zero divisors is a division
ring. (A ring has no zero divisors if ab = 0 implies a = 0 or b = 0.)
- 3.
- Show that there are no simple groups of order 300.
- 4.
- Let R be a commutative domain with field of fractions F.
Prove that F is an injective R-module.
- 5.
- State and prove a structure theorem analogous to the
Fundamental Theorem for modules over a PID, which describes finitely
generated
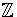 /n
/n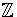 -modules.
(You may assume the Fundamental Theorem
for any argument.)
-modules.
(You may assume the Fundamental Theorem
for any argument.)
- 6.
- Assume that K/F is a Galois field extension and
a
lies in an algebraic closure of K.
Prove that |Gal(K/F)| divides
|Gal(K(a)/F(a))|
deg a, where
deg a
denotes the degree of
a
over F.
- 7.
- Prove that a finite p-group with a unique subgroup of index
p is cyclic. (Hint: first consider abelian p-groups.)
- 8.
- Let f : M - > N be a surjective homomorphism of left
R-modules. Show that if P is a projective R-module, then the
induced map f* : Hom
R(P, M) - > HomR(P, N)
is a surjection of abelian groups.
- 9.
- Let k be a field and let
R = k[X1,..., Xm] be the
polynomial ring in m indeterminates. Prove that if M is a simple
R-module, then dim
kM <
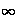 .
.
Peter Linnell
1999-03-05