Algebra Prelim Solutions, Spring 1980

1. We shall use the fundamental theorem for finitely generated abelian groups. We may write
   A = ⊕_i=1ⁿ(Z/q_iZ)^a_i,    B = ⊕_i=1ⁿ(Z/q_iZ)^b_i,    C = ⊕_i=1ⁿ(Z/q_iZ)^c_i
   where a_i, b_i, c_i, n are nonnegative integers, and the q_i are distinct prime powers. Then A⊕B≌A⊕C yields
   ⊕_i=1ⁿ(Z/q_iZ)^a_i+b_i≌⊕_i=1ⁿ(Z/q_iZ)^a_i+c_i
   The fundamental theorem now shows that a_i + b_i = a_i + c_i and hence b_i = c_i for all i. It follows that B≌C as required.

2. Suppose by way of contradiction G is a simple group of order 56. Sylow's theorem for the prime 7 shows that the number of Sylow 7-subgroups is congruent to 1 modulo 7 and divides 8, hence the number of Sylow 7-subgroups is 1 or 8. If there is one Sylow 7-subgroup, x then this subgroup must be normal in G which contradicts the hypothesis that G is simple, consequently G has 8 Sylow 7-subgroups.

   Let A, B be two distinct Sylow 7-subgroups. Then A∩B is a subgroup of A, so by Lagrange's theorem | A∩B| divides | A|, hence | A∩B| = 1 or 7. Now A and B both have order 7, so we cannot have | A∩B| = 7. Therefore we must have | A∩B| = 1. Since every nonidentity element of a Sylow 7-subgroup has order 7, we deduce that G has at least 6×8 elements of order 7.

   Now every Sylow 2-subgroup has order 8, and every element of a Sylow 2-subgroup has order a power of 2 by Lagrange's theorem, so if G has at least two Sylow 2-subgroups, then G has at least 9 elements of order a power of 2. Since we have already shown that G has at least 48 elements of order 7, we now have that G has at least 9 + 48 = 57 elements, which is not possible because | G| = 56. Therefore G has exactly one Sylow 2-subgroup, and so this Sylow subgroup must be normal which contradicts the hypothesis that G is simple.

3. Since we are working over C, an algebraically closed field, we may use the Jordan canonical form. Here every matrix has a unique Jordan canonical form, and two canonical forms are in the same equivalence class of T if and only if they are equal. Since the eigenvalues of a matrix in T are 4,4,17,17,17, the Jordan canonical form of such a matrix must look like

   (

   	4	a	0	0	0
   	0	4	0	0	0
   	0	0	17	b	0
   	0	0	0	17	c
   	0	0	0	0	17

   )

   where a, b, c are 1 or 0, and b = 0 if c = 0. Therefore there are 6 equivalence classes in T.

4. There are many answers to this problem; perhaps the simplest example of a UFD which is not a PID is Z[X]. This is a UFD because Z is a UFD, and a polynomial ring over UFD is again a UFD. We now establish that Z[X] is not a PID by showing that the ideal (2, X) (the ideal generated by 2 and X) is not principal.

   Suppose on the contrary that (2, X) = f for some f∈Z[X]. Then there exist g, h∈Z[X] such that fg = 2 and fh = X. The equation fg = 2 shows that f must have degree 0, in other words f∈Z, and then fh = X shows that f = ±1. Thus we must have (2, X) = Z[X]. Now the general element of (2, X) is 2a + Xb where a, b∈Z[X]. The constant term of 2a must be divisible by 2, and the constant term of Xb must be zero, hence the constant term of 2a + Xb must be divisible by 2. In particular we cannot have 2a + Xb = 1, so 1 ∉ (2, X) and we have the required contradiction.

5. Let G denote the Galois group of x³ - 10 over Q. By Eisenstein's criterion for the prime 2 (or otherwise), we see that x³ - 10 is irreducible over Q, hence G≌S₃ or A₃. Let ω = (-1 + i√3)/2, a primitive cube root of unity. Then the roots of x³ - 10 are ³√10, ω ³√10, and 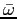$\bar{{\omega}}$ ³√10 ( 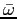$\bar{{\omega}}$ = (-1 - i√3)/2), hence x³ - 10 has one real root and two complex roots, so complex conjugation is an element of G. Therefore G has an element of order 2, which rules out the possibility G≌A₃. Therefore G≌S₃.

   A splitting field of x³ - 10 is Q(i√3,³√10). The normal subfields of the splitting field correspond to normal subgroups of G. The normal subfields corresponding to the subgroups 1 and G are Q(i√3,³√10) and Q respectively. G has exactly one other normal subgroup, namely A₃, so there is exactly one other normal subfield. Since subfields of degree two over Q are always normal, this other normal subfield must be Q(i√3).

6. (a) How to prove this depends on how much field theory one is allowed to assume. Also the result is true without the hypothesis that f is separable. Here is one way to proceed. Suppose K₁, K₂ are fields, θ : K₁ -> K₂ is an isomorphism, g∈K₁[X] is an irreducible polynomial, α₁ is a root of g in a splitting field L₁ for g, and α₂ is a root of the irreducible polynomial θg in a splitting field L₂ for θg (recall if g = a₀ + a₁X + ... + a_nXⁿ with a_i∈K₁, then θg = θa₀ + θa₁X + ... + θa_nXⁿ∈K₂[X]). Then θ extends to an isomorphism φ : K₁(α₁) -> K₂(α₂) such that φ(α₁) = φ(α₂). Using induction on the degree of g, we deduce that φ in turn extends to an isomorphism of L₁ onto L₂. This is what is required.

   (b) Note that x⁴ - 2 is indeed irreducible over Q, by Eisenstein's criterion for the prime 2. The roots of x⁴ - 2 are ± ⁴√2 and ±i ⁴√2. Consider the permutation of the roots ⁴√2 -> ⁴√2, - ⁴√2 -> i ⁴√2 -> -i ⁴√2 -> - ⁴√2. This cannot be induced by an element θ of the Galois group of x⁴ - 2 over Q, because if θ ⁴√2 = ⁴√2, then we must have θ(- ⁴√2) = - ⁴√2.

7. Since Hom_A(M, k) = 0, we must have M = MM. Then Nakayama's lemma yields the result.