- Prove that if f is a separable irreducible polynomial, then the Galois group of f is transitive.
- Show that even though the Galois group of f is transitive,
not every permutation of the roots need occur. (Hint: consider
x4-2 over
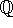 .)
.)
Algebra Preliminary Exam, Spring 1980