Algebra Prelim, May 2006
Do all problems
- Prove that there are no simple groups of order 1755.
- Let P be a finite p-group. Prove that every subgroup of P
appears in some composition series for P.
- Let R be a principal ideal domain. Let A be a finitely
generated R-module and let B be an R-submodule of A. Assume
that there exist nonzero elements r and s of R such that
gcd(r, s) = 1, rB = 0, and s(A/B) is a torsion-free R-module.
Prove that
A @ B
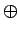 A/B as R-modules.
A/B as R-modules.
- Let
F = Q(i) and let K be the splitting field of x6 - 7
over F.
- (a)
- Determine [K : F] and write down a basis for K over F.
- (b)
- Show that
Gal(K/F) is a dihedral group.
- Let R be a ring with unity 1. Let P be a projective R-module
and let M be an R-submodule of P. Prove: if P/M is a
projective R-module, then M is a projective R-module.
- Let R be a commutative Noetherian ring with unity 1. Let M be a
nonzero R-module. Given
m e M, set
Annm = {a e R | am = 0} and note that
Annm is an ideal
of R. Prove that there exists
s e M such that
Anns is a
prime ideal in R. (Remember: R itself is not a prime ideal in
R.)
- Let
A = C
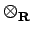 C.
C.
- (a)
- Prove that there is a well-defined multiplication on A that
satisfies the distributive property such that
(
a1 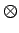 b1
b1)(
a2 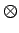 b2
b2) =
a1a2 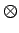 b1b2
b1b2
- (b)
- Now assume that this multiplication makes A into a ring. Prove
that A is not an integral domain.
Peter Linnell
2006-05-22
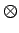 b1)(a2
b1)(a2 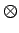 b2) = a1a2
b2) = a1a2 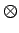 b1b2
b1b2