Algebra Prelim, January 1999
Answer all questions
- 1.
- Let R be a commutative ring with a 1
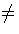 0.
If every ideal of R except the ideal R
is a prime ideal, prove that R is a field.
0.
If every ideal of R except the ideal R
is a prime ideal, prove that R is a field.
- 2.
- Let p and q be distinct primes and let G be a group of
order p3q3. If G has a normal p-Sylow subgroup, prove that
G has a normal subgroup H of order p3q.
- 3.
- Let R be a commutative ring with a 1.
Prove that R is isomorphic
to a proper R-submodule of R if and only if there exists an
element in R which is neither a zero divisor nor a unit.
(A zero divisor is an element r such that there exists
s
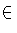 R \ 0
such that rs = 0. A unit in R is an element r
such that there exists s
R \ 0
such that rs = 0. A unit in R is an element r
such that there exists s 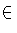 R such that rs = 1.)
R such that rs = 1.)
- 4.
- Let K be a subfield of the field L and let
a
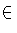 L.
If
[K(a) : K] is odd, prove that
K(a2)
= K(a).
L.
If
[K(a) : K] is odd, prove that
K(a2)
= K(a).
- 5.
- Let p be a prime and let G be an abelian group of order
p6. Suppose the set
{x
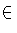 G | xp = 1} has order p2.
Describe all possible groups G (up to isomorphism). Justify your
answer.
G | xp = 1} has order p2.
Describe all possible groups G (up to isomorphism). Justify your
answer.
- 6.
- Let
k
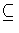 K
K 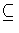 L be fields such that K is a
splitting field over k, and let
s
L be fields such that K is a
splitting field over k, and let
s
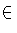 Gal(L/k). Prove that
s(K) = K.
Gal(L/k). Prove that
s(K) = K.
- 7.
- Prove that there is no simple group of order 280.
- 8.
- Let n be a positive integer, let E be a field of
characteristic zero, and let F be a subfield of E such that
[E : F] = n. Prove that
there are at most
2n! fields between F and E.
Peter Linnell
1999-01-15