Since f has at most two roots in K, we see that g and h have at most one root in K. It follows that we may write g = g1g2 and h = h1h2 where g1, g2, h1, h2 are irreducible in K[X], g1 and h1 have degree 1, and g2 and h2 have degree 2. Then f = g1g2h1h2 is the factorization of f into irreducible polynomials in K[X].
Now G/H is a group of order 33 and so the number of Sylow
3-subgroups of G/H is congruent to 1 modulo 3 and divides 11.
Therefore G/H has a normal Sylow 3-subgroup, which we may write as
A/H where A is a normal subgroup of G. Then A is a group of
order 3*59 and the number of Sylow 3-subgroups of A is
congruent to 1 modulo 3 and divides 59. Therefore A has a normal
subgroup K of order 3. Observe that if g ![]() G, then gKg-1
is a subgroup of order 3 contained in gAg-1. Since A is
normal,
gAg-1 = A, so gKg-1 is a subgroup of order 3 in A
and hence
gKg-1 = K, because A has exactly one subgroup of
order 3. Therefore K is a normal subgroup of order 3 in G.
G, then gKg-1
is a subgroup of order 3 contained in gAg-1. Since A is
normal,
gAg-1 = A, so gKg-1 is a subgroup of order 3 in A
and hence
gKg-1 = K, because A has exactly one subgroup of
order 3. Therefore K is a normal subgroup of order 3 in G.
Using exactly the same argument as above with the primes 3 and 11 interchanged, we see that G has a normal subgroup L of order 11. We have now proved that all the Sylow subgroups of G are normal, so G is isomorphic to a direct product of its Sylow subgroups. Also each nontrivial Sylow subgroup has prime order and is therefore cyclic. It follows that G abelian, and then by using the structure theorem for finitely generated abelian groups, we conclude that G is cyclic.
- Obviously
0
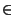 A
A 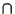 R. Let
a, b
R. Let
a, b 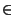 A
A 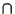 R. Then
a - b
R. Then
a - b 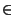 A and
a - b
A and
a - b 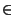 R, so
a - b
R, so
a - b 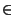 A
A 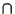 R. Finally let r
R. Finally let r 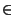 R. Then ar
R. Then ar 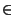 A because A is an ideal of S, and ar
A because A is an ideal of S, and ar 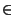 R.
Thus
ar
R.
Thus
ar 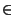 A
A 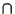 R and we have proved that A
R and we have proved that A 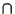 R is an ideal
of R.
R is an ideal
of R.
- Let x
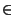 A. Since F is the field of fractions of the PID
R, we may write
x = ab-1 with a, b
A. Since F is the field of fractions of the PID
R, we may write
x = ab-1 with a, b 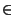 R and (a, b) = 1.
Then there exist p, q
R and (a, b) = 1.
Then there exist p, q 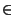 R such that
ap + bq = 1, so
px + q = b-1. Since
p, q, x
R such that
ap + bq = 1, so
px + q = b-1. Since
p, q, x 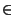 S, we see that
b-1
S, we see that
b-1 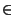 S. Now
A is an ideal of S, so
xb = a
S. Now
A is an ideal of S, so
xb = a 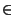 A
A 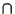 R = Rd, so there exists
r
R = Rd, so there exists
r 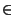 R such that xb = rd. Then we have
x = b-1rd
R such that xb = rd. Then we have
x = b-1rd 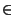 Sd
and the result follows.
Sd
and the result follows.
- We have
[G/M : PM/M] = [G : PM] and
[G : P] = [G : PM][PM : P],
so
[G/M : PM/M] divides [G : P]. Since P is a Sylow p-subgroup
of G, we see that [G : P] is prime to p and hence
[G/M : PM/M] is
prime to p. This shows that PM/M is a Sylow p-subgroup of G.
- Let n
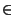 N. Then
nPn-1 = P and
nMn-1 = M, hence
nPMn-1 = PM. This shows that Mn is in the normalizer of PM/M
in G/M and we conclude that n
N. Then
nPn-1 = P and
nMn-1 = M, hence
nPMn-1 = PM. This shows that Mn is in the normalizer of PM/M
in G/M and we conclude that n 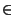 H. The result follows.
H. The result follows.
- The number of Sylow p-subgroups of G/M is
[G/M : H/M] = [G : H], and the number of Sylow p-subgroups of G is [G : N].
Since
N
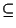 H, we see that [G : H] divides [G : N] and the
result follows.
H, we see that [G : H] divides [G : N] and the
result follows.
- A5 X
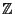 /59
/59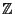 .
.
-
 /2
/2 X
X
 /2
/2 X
X
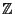 /885
/885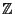 .
.
| G | ||
| H |
for certain integers a, b, ai, bi, n, and the pi are distinct primes. Since G