Algebra Prelim, January 1998
Answer all questions
- Let F and K be fields of characteristic 0 with K an
extension of F of degree 21. Let f (x) be a polynomial in F[x]
of degree 6 which has no roots in F and exactly two roots in K.
- Describe the factorization of f (x) into irreducible
polynomials in F[x].
- Describe the factorization of f (x) into irreducible
polynomials in K[x].
- Let G be a group of order
1947 = 3*11*59. Prove that G is
cyclic.
- Let G be a group of order pn with n
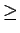 2 and p prime.
Prove that G has a normal abelian subgroup of order p2.
2 and p prime.
Prove that G has a normal abelian subgroup of order p2.
- Let
K =
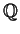 (
(![$ \sqrt[3]{2}$](img3.gif) ,w) where
w = cos(2p/3) + isin(2p/3) is a primitive cube root of unity.
,w) where
w = cos(2p/3) + isin(2p/3) is a primitive cube root of unity.
- What is
[K :
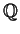 ]?
]?
- Prove that
K/
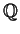 is a Galois extension.
is a Galois extension.
- Describe the Galois group of
K/
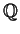 .
.
- Let R be a PID with field of fractions (quotient field) F,
let S be subring of F which contains R, and
let A be an ideal of S.
- Prove that A
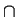 R is an ideal of R.
R is an ideal of R.
- If
A
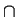 R = Rd, prove that A = Sd. (Hint: if a/b
R = Rd, prove that A = Sd. (Hint: if a/b 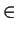 S
with (a, b) = 1, prove that 1/b
S
with (a, b) = 1, prove that 1/b 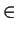 S.)
S.)
- Let p be a prime, let a, k be positive integers such that
p does not divide k, and let G be a group of order pak. Let
M be a normal subgroup of G and let P be a Sylow p-subgroup of
G.
- Prove that PM/M is a Sylow p-subgroup of G/M.
- Let H/M be the normalizer of PM/M in G/M and let N be
the normalizer of P in G. Prove that
N
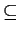 H.
H.
- Prove that the number of Sylow p-subgroups of G/M is a
divisor of the number of Sylow p-subgroups of G.
- Give an example of a group of order
3540 = 59*60 = 59*5*3*4
which is not solvable.
- Give an example of a group of order 3540 which is solvable but
not cyclic.
- Let G and H be finitely generated abelian groups such that
G
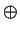 G
G 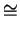 H
H 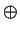 H. Prove that G
H. Prove that G 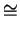 H.
H.
Peter Linnell
1999-06-16
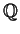 ]?
]?
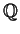 is a Galois extension.
is a Galois extension.
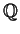 .
.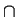 R is an ideal of R.
R is an ideal of R.
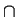 R = Rd, prove that A = Sd. (Hint: if a/b
R = Rd, prove that A = Sd. (Hint: if a/b 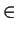 S
with (a, b) = 1, prove that 1/b
S
with (a, b) = 1, prove that 1/b 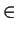 S.)
S.)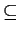 H.
H.